Physical properties of the Earth's interior

A primary application of seismology is the determination of the structure and constitution of the Earth's interior from measurements made at the surface. Fundamental to this problem is the determination of the changes in density with depth. The density depends on the pressure, temperature and an indefinite number of variables specifying the chemical composition. Since the stress in the Earth's interior is essentially equivalent to a hydrostatic pressure, the variation in pressure with depth is a straightforward mathematical function.

If further simplifying assumptions are made concerning temperature and chemical homogeneity it is possible to derive another equation linking density with depth. This equation was first obtained by Adams and Williamson in 1923 and may be integrated numerically to obtain the density distribution in those regions of the Earth where chemical and other variations may be neglected.

Additional information on the physical properties of the Earth's mantle and core may be obtained from an analysis of the free oscillations of the Earth. If a bell is struck with a hammerit rings. The Earth also rings when it is disturbed by a great earthquake and the entire globe vibrates like a bell for as long as several weeks. The tones of the Earth's vibrations are pitched too low for the human ear to hear, but modern seismographs are sensitive enough to detect these low frequency oscillations.

There are two classes of such oscillations, torsional (or toroidal) and spheroidal (Figure 3.11). In the simplest torsional mode there is no displacement at the equator, and the two hemispheres oscillate in antiphase. The fundamental spheroidal oscillation is an alternating compression and rarefaction of the whole Earth. The next higher mode is the football' mode. The nodes are two parallels of latitude dividing the surface into three zones. As the sphere oscillates it is distorted alternately into an oblate and prolate spheroid. Its period is 53 minutes, corresponding to E flat in the twentieth octave below middle C. There are higher modes with an increasing number of subdivided zonal distributions, and each of these modes also has overtones with internal nodal surfaces.

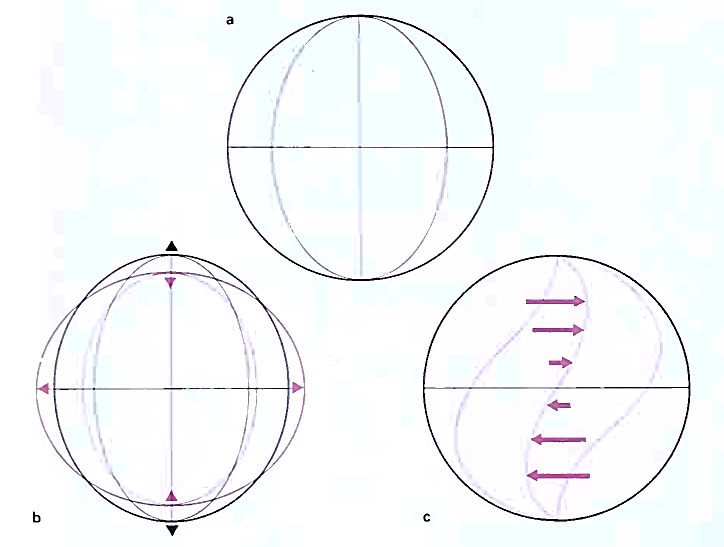
3.11: The static Earth (al and two classes of free oscillation (b and c)

Free oscillations of the Earth were first observed in 1952. Although it was not until the great Chilean earthquake of 22 May 1960 that improved instrumentation enabled detailed measurements to be made. Additional results were obtained from the great Alaska earthquake of 28 March 1964. Although the free oscillations of a uniform elastic sphere were first investigated more than a hundred years ago. calculations for realistic Earth models, taking into account detailed structure, gravitational forces and rotation, were not undertaken until fairly recently.

Such calculations would have been impossible without the aid of modern computers. The free oscillations excited by a major earthquake last for several days, but their amplitude diminishes because the Earth is not a perfectly elastic body. The precise way in which it diminishes can be determined for each mode of oscillation and information on the elastic properties of the Earth's interior obtained.

It should be noted, however, that the average' Earth to which the average periods of free oscillation modes relate is not necessarily the same as an Earth model to which the currently available average travel times of seismic body waves apply. This is because earthquake epicentres and recording stations are not randomly distributed over the Earth's surface. It must also be stressed that since the variations in the physical properties of the Earth are in general continuous, and the amount of data available is finite, there is no unique solution to the problem, which is further compounded by the fact that the data themselves contain errors. However, it has proved possible to place bounds on possible solutions, and certain properties of the Earth are known to a high degree of accuracy.

For example, the pressure distribution may be obtained once the density distribution has been determined. Since the density is used only to determine the pressure gradient the pressure distribution is insensitive to small changes in the density distribution and may be determined quite accurately. The variation with depth of the gravitational acceleration (g) can also be calculated. Its value does not differ by more than 1 per cent from 9.9 m per second per second (its value at the Earth's surface: see Chapter 6) until a depth of over 2400 km is reached.

On the other hand values of g deep within the Earth are highly dependent on density, and calculated values for depths below 4000 km may be in error by as much as 5 per cent. From a knowledge of the density distribution, values of the elastic constants can be computed.

Even if the variation of density and other physical properties through the Earth were known in detail, laboratory experiments on rocks and minerals are necessary to identify the materials in the Earth's interior. Studies of wave propagation measurements in rocks show that the velocity of compressional waves depends principally upon density and mean atomic weight.

However, most common rocks have mean atomic weights close to 21 or 22 regardless of composition, and rocks or minerals of very different compositions may have the same densities and seismic velocities. Thus it is not easy to infer chemical composition from seismic data alone, and laboratory experiments conducted in the conditions of pressure and temperature that exist deep within the Earth are necessary.

The pioneering experimental work of Bridgman. beginning in the 1920s, was undertaken at pressures up to 100 kilobars, which corresponds to a depth of only 300 km within the Earth. However, in the past few years, dynamic determinations of the compressibility of minerals and rocks have been made by a number of researchers up to pressures in excess of those at the centre of the Earth. Such high pressures are created for very short time intervals behind the front of a strong shock wave set up by an explosive charge.

They are an order of magnitude greater than those that can be obtained by static methods. Although the pressures are maintained for intervals of usually less than a microsecond this is long enough to allow measurements to be made of some geophysically important quantities. More recently, sustained high pressures and temperatures have been made possible by the refinement of the diamond-anvil pressure cell, an instrument in which two tiny diamond faces are squeezed together with a solid sample in between.

Previously, high pressures were obtained by applying very large forces to relatively large surface areas. In the new technique high pressures are generated by applying modest forces to very small areas (a few hundred micrometres in diameter). A problem in this approach is the possible failure of the diamonds themselves. Even carefully selected and shaped diamonds will crack and shatter into diamond dust if not properly aligned and supported. Pressures of 1.7 megabars, equivalent to that just below the core-mantle boundary, have been obtained. At these pressures the diamonds (the hardest substance known) began to deform.