The Doppler Effect. Description

The galaxies in the night sky appear static until they are studied spectroscopically. Astronomer Vesto Slipher discovered that the spectra of galaxies display spectral absorption lines which have been shifted from their measured laboratory wavelengths.

This can be explained as the optical equivalent of the Doppler effect. We are all familiar with the way in which bells and sirens change pitch as they pass us. Instead of thinking of cars and trains which emit sound, let us transpose the idea to starships and light rays.

Imagine two starships heading out into deep space. Initially, they are both travelling with the same velocity, although starship A is in front of starship B. Atop each of the spacecraft is a flashing light. Both regularly pulse on and off with a frequency, f. Someone on starship В can see both the flashing light on his ship and the one on starship A.

If this person measures the frequency of both lights it will be found that they are the same. If starship A suddenly increases to another velocity and the frequencies of the two flashing lights are compared again, it will be noticed that f_A is smaller than f but that f_B remains the same (i.e. equal to f). Thus, a fundamental change in the way observers on starship В perceive starship A has taken place simply because there is now a difference in velocity between the two vessels.

This concept is at the heart of Einstein’s special relativity and is a direct consequence of light possessing a finite invariant velocity through space. Does this mean that the flashing light has actually slowed down or does it just mean that starship В perceives it to slow down? This is where the concept of relativity comes into play. The flashing light on starship A appears to slow down only to observers in motion away from it. It does not matter whether the observer is moving away or starship A is moving away or both are moving away from each other.

All that matters is that they are in relative motion away from one another (i.e. the distance between them is increasing with time). The exact amount by which the flashing light slows down is then dependent upon how fast they are separating. Since it does not matter which starship is moving, from an observer on starship A’s point of view, it is the flashing light on starship В which has slowed down, not the one on starship A! The concept is easy to grasp through some elementary mathematics.

If two observers - one on each vessel - agree to time the flashes of starship A’s light, then observer A records a time t_A1 as soon as the light flashes on (see Fig. 3. 6). The observer on starship В begins timing after the light has crossed the distance, d, between the two ships. Hence, the time recorded by observer В is :

When observer A sees the second flash a second time, t_A2 is recorded. Thus the time between flashes, as timed by observer A, is

τ is known as the ‘proper time’ because it is the time of the flashes as observed from the light’s own frame of reference (i.e. there is no relative motion between the light and the observer). The observer on starship В records a time of

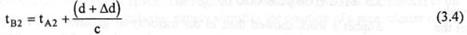
This distance, Δd, is how far the starships have parted in the proper time, τ. From equations (3.2) and (3.4), the time interval, Δt, between flashes as measured by observer В can be seen to be

Thus, the increase in the length of time between flashes is proportional to the increase in distance between the two ships which, in turn, is proportional to the relative velocity between the two ships. If the distance decreases, i.e. the starships are getting closer together, then Δd will be negative and Δt < τ.

It is important to remember that this section has analysed what observers A and В see of the flashing light on starship A. If it were recast to analyse the appearance of the flashing light on starship B, it would be observer A who saw the increased time, not observer. B. This reinforces the fact that these are observational effects which have to be taken into account when we observe objects in relative motion to us.