Justification of Advanced Manufacturing Systems

According to Meredith and Suresh (4), investment justification methods for advanced manufacturing technologies are classified into economic analysis techniques, analytical methods, and strategic approaches. These methods deviate from each other mainly because of the treatment of nonmonetary factors. Economic justification methods for manufacturing investments have been discussed thoroughly in the past couple of decades.

Economic analysis methods are the basic discounted cash flow (DCF) techniques, such as present worth, annual worth, internal rate of return, and so on, and other techniques such as payback period and return on investment. It is well known by practitioners who follow the fundamental principles of engineering economy that accounting methods, which ignore time value of money, would produce inaccurate or at best approximate results.

The conventional DCF methods do not seem to be suitable on their own for the evaluation of an advanced manufacturing technology (AMT) investment because of the nonmonetary impacts posed by the system. Sullivan (5) points out the inadequacy of traditional financial justification measures of project worth such as return on investment, payback, and net present worth in considering the strategic merits of advanced manufacturing technologies.

The results of the surveys conducted by Lefley and Sarkis (6) for appraisal of AMT investments in the United Kingdom and United States indicate the support for the difficulty in assessing AMT investments because of their nonquantifiable benefits.

Because of this difficulty, over 80 % of the respondents in the United States and United Kingdom point out that not all potential benefits of AMT investments are considered in the financial justification process. Improvements in product quality, reliability, productivity, precision, cycle times, and competitiveness as a result of the versatility and flexibility of the system, are the focal points in the justification stage of an AMT investment. Productivity, quality, flexibility, and other intangibles should be examined in terms of potential returns through enhancement of long-term business competitiveness as well as in terms of a comprehensive evaluation of internal costs.

When flexibility, risk, and nonmonetary benefits are expected, and in particular if the probability distributions can be estimated subjectively, analytical procedures may be used. Strategic justification methods are qualitative in nature, and they are concerned with issues such as technical importance, business objectives, and competitive advantage (4). When strategic approaches are employed, the justification is made by considering long-term intangible benefits. Hence, using these techniques with economic or analytical methods would be more appropriate.

Figure 1, which is an updated version of the classification provided in Karsak and Tolga (7), resumes the justification methods for advanced manufacturing technologies. Axiomatic design approach (8,9), digraph and matrix methods (10), and QFD and fuzzy regression (2) can be listed as the major updates to the classification given in Ref. 7.

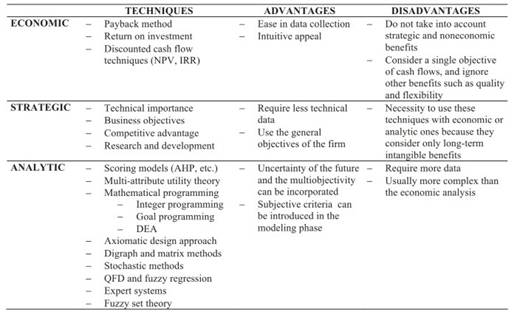
Figure 1. Classification of justification methods for advanced manufacturing technologies (7)

Over the past several decades, manufacturing firms have assigned an increasing importance to robot selection because improper selection of robots can adversely affect their productivity and product quality along with profitability. The increased use of robots and the complexity of the robot evaluation and selection problem have motivated the researchers to develop models and methodologies for making sound decisions.

Mathematical programming, statistical procedures, and fuzzy set theoretic methods, as well as multiattribute and multiobjective decision-making methods can be listed among analytical methods used for robot selection. More recently, axiomatic design approach, digraph and matrix methods, and quality function deployment (QFD) and fuzzy regression have also been proposed as alternative decision aids. Many classifications for models developed for robot selection are available in the literature.

For instance, Khouja and Offodile (11) classified models for robot selection as multicriteria decision-making models, performance-optimization models, computer-assisted models, statistical models, and other approaches. Here, we briefly review expert system applications and the use of multicriteria decision making (MCDM) techniques, which possess the potential for considering the multiple and conflicting criteria inherent in the robot selection problem.

Relatively few studies exist regarding the use of expert systems in robot selection. Fisher and Maimon (12) developed a two-phase model for robot selection. In phase 1, an expert system is used to obtain a list of tasks’ requirements. The expert system determines a set of robotics technologies and engineering specifications that meet the requirements. In phase 2, a list of candidate robots is chosen and ranked. Boubekri et al. (13) developed a computer-aided system for robot selection, which includes an expert system that considers the functional and organizational parameters specified by the user, an economic feasibility analysis module based on payback period, and a module that provides the user with a detailed description of each robot in the knowledge base.

Agrawal et al. (14) employed an expert system to determine the set of important attributes for the particular application and narrow down the robot alternatives, and then used a multiattribute decision-making approach named TOPSIS, which is based on the ideal solution concept, for ranking the shortlist of robot alternatives.

Several articles have focused on the use of MCDM techniques for justification of industrial robots. Imany and Schlesinger (15) compared linear goal programming and ordinary least-squares methods via a robot selection problem in which robots are evaluated based on cost and technical performance measures, which include load capacity, velocity, and repeatability. Liang and Wang (16) presented a robot selection procedure using the concepts of fuzzy set theory.

Although providing a multicriteria tool that can incorporate subjective criteria, their approach suffers from the implicit assumption of mutual independence of technical performance parameters. Khouja (17) used DEA and MAUT in a two-phase procedure for robot selection. Baker and Talluri (18) addressed some limitations of the simple radial efficiency scores used for ranking industrial robot alternatives in Khouja’s study and proposed a more robust evaluation procedure based on crossefficiency analysis, which is an extension used for improving the discriminating power of DEA.

Goh (19) presented an AHP model for a group of decision makers that considered both subjective and objective factors for robot selection. Karsak (20) developed a two-phase decision framework that employs DEA in the initial phase to determine the technically efficient robot alternatives and a fuzzy robot selection algorithm in the second phase to rank the technically efficient robots. Parkan and Wu (21) studied the robot selection problem using operational competitiveness rating, TOPSIS, and utility function model, and proposed to rank the robot alternatives based on the averages of the rankings obtained by these three decision aids.

Braglia and Petroni (22) proposed the use of DEA with restricted multiplier weights for identifying the optimal robot by considering cost as the single input and engineering attributes as the outputs, and they addressed the advantages and drawbacks of using weight-restriction constraints compared with those of cross-efficiency analysis. Talluri and Yoon (23) proposed a cone-ratio DEA approach for robot selection, which made use of weight-restriction constraints to incorporate a priori information on the priorities of factors.

More recently, a practical common weight MCDM methodology with an improved discriminating power has been developed for robot selection (24). The merits of the approach proposed in the paper compared with DEA-based models can be summarized as its ability to evaluate all robot alternatives by common weights for performance attributes that overcome the unrealistic weighting scheme common to DEA resulting from the fact that each decision-making unit (DMU) selects its own factor weights to lie on the efficient frontier, and to further rank DEA-efficient DMUs with a notable saving in computations compared with cross-efficiency analysis.