Electromagnetic Spectra. The Production of Emission, Absorption, and Continuous Spectra

The entire gamut of electromagnetic radiation is known today as the electromagnetic spectrum. The word spectrum was first coined by Isaac Newton, who was the first person to produce and study the optical spectrum. The word itself is Latin for ‘ghost’ or ‘apparition’, and was used by Newton to describe the ephemeral pattern of colours which danced on the wall of a darkened room when he placed a prism in the path of a light beam.

Initially, the spectra observed were simply continuous bands of colour. In 1802 W.H. Wollaston observed a few dark lines in the solar spectrum and assumed that they were gaps between the colours, but in 1814 Joseph Fraunhofer magnified a spectrum of sunlight and discovered that it was full of the dark lines of the absorption spectrum. Later that century, emission spectra were observed by two chemists, Robert Bunsen and Gustav Kirchhoff.

They passed the light from chemical flame tests through a prism and discovered that their spectra were simple patterns of coloured lines rather than dark lines superimposed upon continuous colours. Further investigations showed that each element had a characteristic pattern of these emission lines. It was also realised that every emission spectrum had a corresponding absorption spectrum (see Fig. 2. 3).

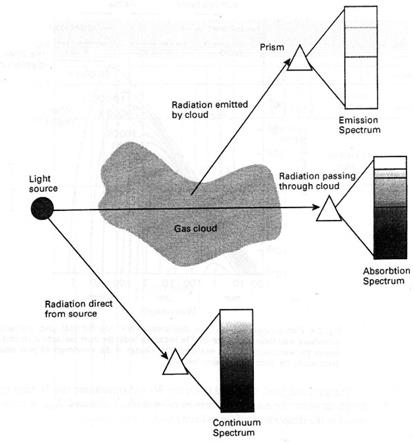
Fig. 2. 3. The production of emission, absorption, and continuous spectra. The continuous spectrum is produced by a hot, solid body or by a hot, dense gas. Emission spectra are produced by a hot, tenuous gas, and absorption spectra are produced by cold clouds of tenuous gas

It appeared that, in some way, atoms could only absorb and emit at specific wavelengths of radiation. By now, physicists also recognised that a truly continuous spectrum was only produced by heating an object and letting it radiate that heat as electromagnetic radiation. Thus, this method of producing electromagnetic radiation became known as thermal emission.

Thinking of light as a wave, however, made it impossible to understand why atoms and radiation should behave in this way. The production of thermal radiation is characterised by three empirical laws which assume that the object being heated is a perfect absorber (and perfect emitter) of radiation. Since a perfect absorber would not reflect any radiation, its colour would be black.

Thus, an object of this type has become known as a black body. All radiation absorbed by the object will be converted into heat energy and then re-radiated at lower frequencies. As well as a solid object at a specific temperature, a dense ideal gas can also radiate as a black body if its constituent atoms and molecules are in thermal equilibrium. In most astronomical and cosmological cases, it is emission by a dense ideal gas in thermal equilibrium which produces black body radiation.

For instance, stars are well approximated as being black bodies and, as we shall see, the cosmic microwave background radiation is also characterised by a black body curve. Hence, from now on, this book will assume that Planck (black body) curves are being produced by dense ideal gases in thermal equilibrium.

The first law which describes the process of black body thermal emission is known as the Stefan-Boltzmann law. It gives the total radiated power per unit area, R, for a black body at a given temperature, T.

R = σT⁴ (2. 2)

The proportionality is maintained by the Stefan-Boltzmann constant, σ = 5.67 x 10^-8W/m²K⁴.

The second law is known as the spectral radiancy and describes how the intensity of radiation changes with wavelength and temperature. Graphs constructed for the spectral radiancy at specific temperatures are known as Planck or black body curves (see Fig. 2. 4). When the spectral radiancy is integrated over all wavelengths it equals the Stefan-Boltzmann law.

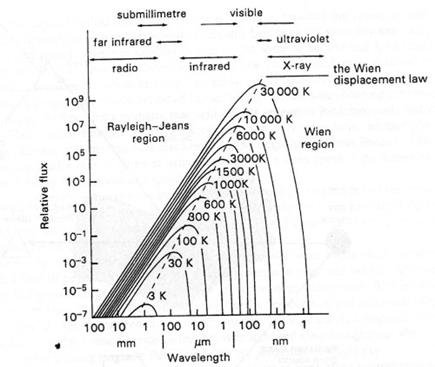
Fig. 2. 4. Planck curves and the Wien displacement law. Any hot body gives out radiation in accordance with these Planck curves. The hotter the body, the more radiation is emitted and the shorter the wavelength of peak emission. This change in the wavelength of peak emission is described by the Wien displacement law.

The third and final, empirical law is the Wien displacement law. It states that the wavelength at which the maximum intensity of radiation is released, is inversely proportional to the temperature of the radiating body.

The Wien constant, w, is equal to 2898 μm K.

At the turn of this century, physics was facing the challenge of finding a formula which could fit the Planck curves and be totally derivable from a theoretical basis. The best attempt at fitting the curve that classical physics could offer was the attempt made by Lord Rayleigh and later modified by James Jeans. It could only fit the curves at very long wavelengths. A second attempt, made by Wilhelm Wien, fitted better at shorter wavelengths but failed to fit at long wavelengths. Wien departed somewhat from classical theory, however, by assuming that there was an analogy between the spectral radiancy curves and the Maxwell speed distribution curves for the molecules of an ideal gas.

Max Planck solved the problem by interpolating between the two models and presenting a formula which fitted the radiation at all wavelengths. He then set out to derive his equation again, this time from a simple set of theoretical assumptions. He succeeded brilliantly and presented his theoretical equation which perfectly matched the spectral radiancy curves.

His equation used two new constants, namely, the Boltzmann constant, к = 1.38 x 10^-23J/K and the Planck constant, h = 6.63 x 10^-34Js. In order to produce his equation, Planck had to make a radical assumption about the way in which atoms release radiation. Classically, it had been assumed that atoms could emit radiation of any energy. Max Planck introduced the idea that atoms could only release radiation at certain predefined energies.

Albert Einstein proposed that light could sometimes be thought of as particles known as photons and, turning the tables, Erwin Schrödinger proposed that matter could sometimes be thought of as waves. Using these ideas, which became generically known as quantum theory, Niels Bohr explained the possible positions an electron could assume around a hydrogen nucleus by consideration of their emission spectra. The photon concept allows the energy carried by each photon, E, to be calculated in terms of the light’s frequency, f. E = hf (2. 5).

The key to quantum theory is wave-particle duality. It states that light, traditionally thought of as a wave, can sometimes be a particle and that electrons, traditionally thought of as particles, can sometimes behave as waves. As physicists and astronomers, we are free to regard light and electrons as particles or waves in order to solve the problem at hand. This seems like quite a fundamental liberty to take on the part of the scientists and the question naturally arises: what is an electron, really? Is it a wave or a particle? The answer is that, just like light, it is both and yet neither.

Quantum theory states that everything has both a particle nature and a wave nature. This very book is not just a solid object but is a wave formation as well. The key to why it behaves like a solid object, however, is because it is very much more massive than an electron. Electrons contain such tiny masses that when the quantum theory equations for their behaviour are solved, neither wave nature nor particle nature shows dominance. Hence, it displays the qualities of both. If the quantum equations were solved for this book, however, it’s solid particle-like nature would overwhelm the wave nature.

The concept of quantization and wave-particle duality has shown that electrons can only exist around atomic nuclei in certain states defined by the quantum nature of the atom. When radiation comes into contact with electrons around atoms, the photon will be absorbed only if it contains enough energy to allow the electron to jump to a new energy state. Later, when the electron jumps back down to its original level, the energy is given back out as a photon with a specific wavelength. Thus, the process responsible for the production of absorption and emission spectra is finally understandable, and the reason why there are line spectra follows naturally from the explanation.

The production of line spectra occurs because the electrons are jumping between quantized energy levels, but at no stage are the electrons losing their association with their parent nuclei. Thus, these transitions are known as bound-bound transitions (see Fig. 2. 5).

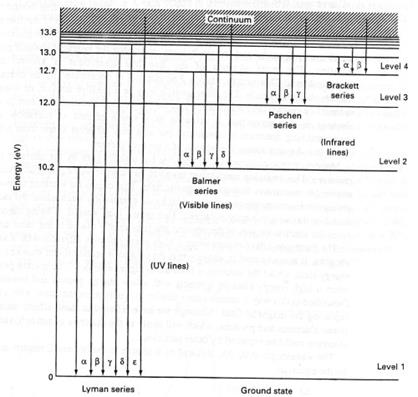
Fig. 2. 5. Energy levels and transitions within the hydrogen atom. In the simple Bohr picture of the atom, energy levels are said to be quantized, i.e. the electrons may take up only certain specific energies. For the hydrogen atom, an energy level diagram can be drawn showing all available energy levels and the series of spectral lines (e g. Lyman, Balmer, Paschen and Brackett) produced by transitions between them. Electrons jumping from higher to lower energy levels produce emission lines, while those jumping from lower to higher energy levels produce absorption lines

An ideal gas can radiate either a continuous black body spectrum or a line spectrum, depending upon the density of the gas cloud. A tenuous gas has negligible reactions between its constituent atoms and so the predominant way in which radiation is either absorbed or emitted depends only upon the way in which the electrons interact with the surrounding photons. This leads to emission and absorption spectra. In a dense gas the energy levels are altered by the proximity of the atoms to one another, and this smears the radiation out into a continuous band, producing a continuum.

Spectral lines have a characteristic shape known as a Gaussian profile. This is because there is a natural tendency for the lines to spread out over a small range of wavelengths. For the atoms in an ideal gas, the temperature of the cloud will translate directly into a velocity distribution for its constituent atoms. When an electron absorbs and then re-emits a photon of radiation, the wavelength of the photon will be slightly altered by the individual motion of the emitting atom.

When the cloud is studied as a whole, the statistical distribution of velocities (described by Maxwell) creates these Gaussian profiles. The process is known as thermal Doppler broadening. In the case of turbulent motion within the cloud being studied, turbulent Doppler broadening will also take place. The analysis of the shape of spectral lines can therefore tell us what physical conditions are possessed by the emitting (or absorbing) cloud.

As the density of the cloud increases, the atoms become more crowded and the amount of interaction between them becomes significant. Our first clue can be found by remembering that one of our conditions for black body radiation was that the cloud must be in thermal equilibrium. This implies that there must be a large number of atomic interactions in order to spread the thermal energy evenly between atoms in the gas. In the course of these collisions, the atoms will interact with each other. This occurs because the wave nature of the electrons allows it to act as if its charge is distributed evenly about the atomic nucleus. Thus the region in which the particulate electron must be located is known as the electron cloud.

The atoms in a dense ideal gas which is in thermal equilibrium interact by feeling a repulsive force between their surrounding electron clouds. This alters the motion of the interacting electrons causing a corresponding change to the energy of the system. That energy is lost in the form of a photon. For our purposes we can think of the energies involved in these processes as being unquantized and so the radiation is emitted in a continuum which, because of the distribution of atomic energies, gives a Planck curve.

So, the careful analysis of the spectrum from any celestial object can tell us a a great deal about the matter contained within the object under scrutiny. The shape of the spectrum, the presence or absence of spectral lines and the intensity of radiation all help in understanding the physical processes by which the radiation was emitted.