Ultrasonic Effects on Porous Media

Wave Propagation in Porous Media. Mechanical waves propagate through media with elastic properties. Energy is absorbed and translated by adjoining molecules along the wave trajectory. A longitudinal wave oscillates in the direction of propagation. The Biot-Stoll theory describes wave propagation in fluid-saturated porous media. Biot discovered three characteristic waves: two fast waves, one longitudinal and one shear, which propagate with little dispersion, and a slower and highly attenuated longitudinal wave. Biot’s models assume viscoelasticity in porous media. Stoll employed Biot’s theory to show wave attenuation in saturated media caused by frictional losses from intergranular contact and viscous losses from pore fluid motion in relation to the media. Energy losses are also produced by sound energy absorption by porous media.

Wave attenuation is monitored by measuring sound intensity as pressure amplitude via an oscilloscope. Sound intensity, I (W m^-2), is:

in which P is the acoustic pressure (Pa), p is the density of the medium (kg m^-3), and c is the speed of the sound wave (m s^-1). Acoustic impedance, Z, is an intrinsic property to the medium defined by Z = pc.

Intensity attenuation is both intrinsic to the medium and a function of irradiation distance. Intensity attenuation is defined by:

where I_o is the initial intensity (W m^-2), a is the media-specific attenuation coefficient, and L is the distance from the source (m). As the distance from the source increases, attenuation increases and intensity decreases.

Fluid Flow Effects. The slow, longitudinal wave described by the Biot-Stoll theory causes the interstitial pore fluid and porous media to move out of phase [102]. The oscillating pore water enhances liquid flow through porous media. Mechanical vibrations on pore walls increase media permeability, altering pore radii and inducing “peristaltic transport". Moreover, pulsed sonication enhances permeability 10-15 times more than continuous sonication. Enhanced fluid flow is also due to acoustic energy dissipation in pore water. Localized heating lowers pressure gradients and fluid viscosities. Therefore, pore flow enhancement by ultrasound is dependent on media porosity, fluid viscosity, and hydraulic gradient.

Liquefaction of water-saturated soils occurs due to increases in stress such as that provided by ultrasound or other pressure waves. The increased stress causes pore water increases. Highly permeable soils drain immediately but low-permeability soils do not and, consequently, liquefy. Following liquefaction, the soil consolidates and has a lower permeability. Thus, it may be possible that the permeability is decreased after sound and ultrasound application due to oscillating stresses of the sonic or ultrasonic wave.

Solute Transport. The physical processes that govern transport of a conservative solute from a source (e.g. an injection point) in porous media are advective and dispersive flux. Advective flux is the solute movement in the direction of bulk fluid flow. Dispersive flux is spreading and movement of solute caused by diffusion and dispersion. Enhanced pore flow by ultrasound increases mass fluxes for enhanced solute transport.

One-dimensional solute transport in porous media is modeled using the convective dispersion equation (CDE) under steady-state conditions. Steady-state flow conditions occur in the absence of perturbations. The base CDE expression with linear adsorption is:

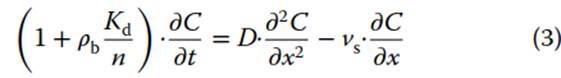
where C is the aqueous-phase solute concentration (mgL^-1), t is the time (h), p_B is the bulk density of the media (gL^-1), n is the porosity, K_d is the equilibrium soil/sediment-water partition coefficient (L g^-1), x is the coordinate parallel to flow (cm), D is the hydrodynamic dispersion coefficient (cm² h^-1), and v_s is the seepage velocity (ms^-1). The factors in the parentheses on the left side of the equation, 1 + p_bK_d/n, are equivalent to the retardation coefficient, R.

Enhanced solute transport due to ultrasound has been demonstrated by improved breakthrough curves in water-saturated columns packed with glass beads.

Ultrasound enhances v_s and D coefficients of the 1 - D CDE equation shown by: v_e = v_s + v and D_e = D + D, where v_e and D_e are the effective coefficients. v* and D* are the enhancements due to ultrasound. The enhancements of seepage velocity and dispersion coefficients relate to increases in advection and dispersion, respectively.