The demonstrating of a prick, a straight line, a circular line, and to raise or let fall a perpendicular, the one line parallel to another

Before I proceed unto the several lines in a ship's body, I do think it not amiss, for the sake of those who may be desirous, to learn what is intended for instruction, namely to show them the full art of measuring all sorts of figures and shapes, both superficial and solid, together with the art of gauging, and the rule static, as well by geometry as by arithmetic, which being attained unto, I conceive those who intend to build ships may be the more apt to proceed without difficulty.

So that it may be better understood, I do begin in a short method, only laying down one demonstration in every part of my work, until I have finished what I have promised, whereby those who have not the use of arithmetic may be gainers by their labours, as those who have made great use thereof. And so proceed unto the laying down to a point, which is the first

work to be understood in our art.

A point or prick is the least dimension and cannot be divided, it being the smallest matter you can conceive in your mind or demonstrate, and its use is mostly, in this work, a centre whereby you describe either circle or parts, and is demonstrated as you find it, by a small prick with the letter A.

Having showed you a point as aforesaid, do proceed unto a line. A line is length and not breadth or thickness, and may be divided from A to B equal or unequal, as from A to C unequal, and from C to B equal, as for example ACB. From A to C the line is divided into three unequal parts, but from C to B into two equal parts, and thus you are shown what a line is, namely a straight line, which is the shortest of lines. There are other lines, as circular lines, whereof great use will be made in our work, and therefore I shall show what is called a circular line, as, for example, take a pair of compasses and set one leg at A and open them at any distance, and with the other leg of your compasses describe an arc or a piece of a circle, and that line is a circular line, or a segment of a circle, as the line BCD.

Which is all I shall say as to lines straight or circular, conceiving these appear very plain. I do proceed to the next, having already showed what a straight line is and also a circular, as is manifest by the two problems in the margin.

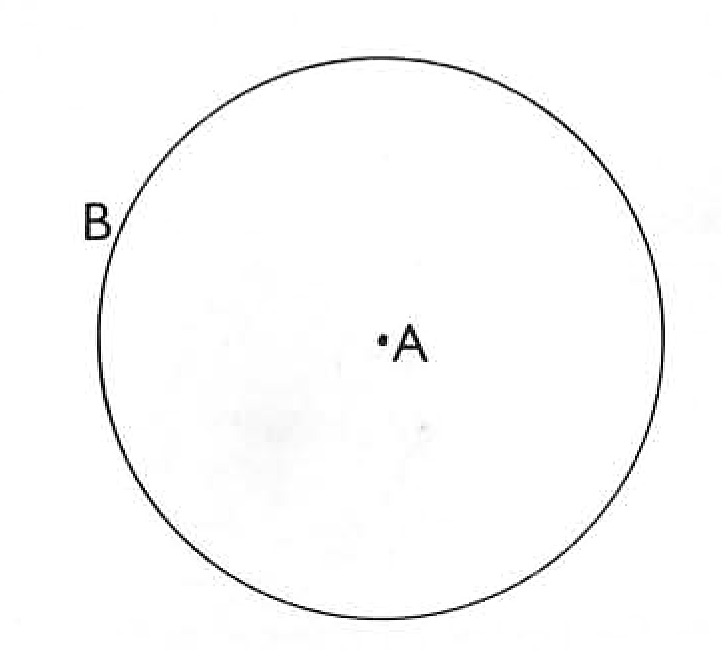
A circle is performed by opening your compasses at any distance. Setting one leg in A, strike a line beginning at B. Continue it round A until it meet at B.

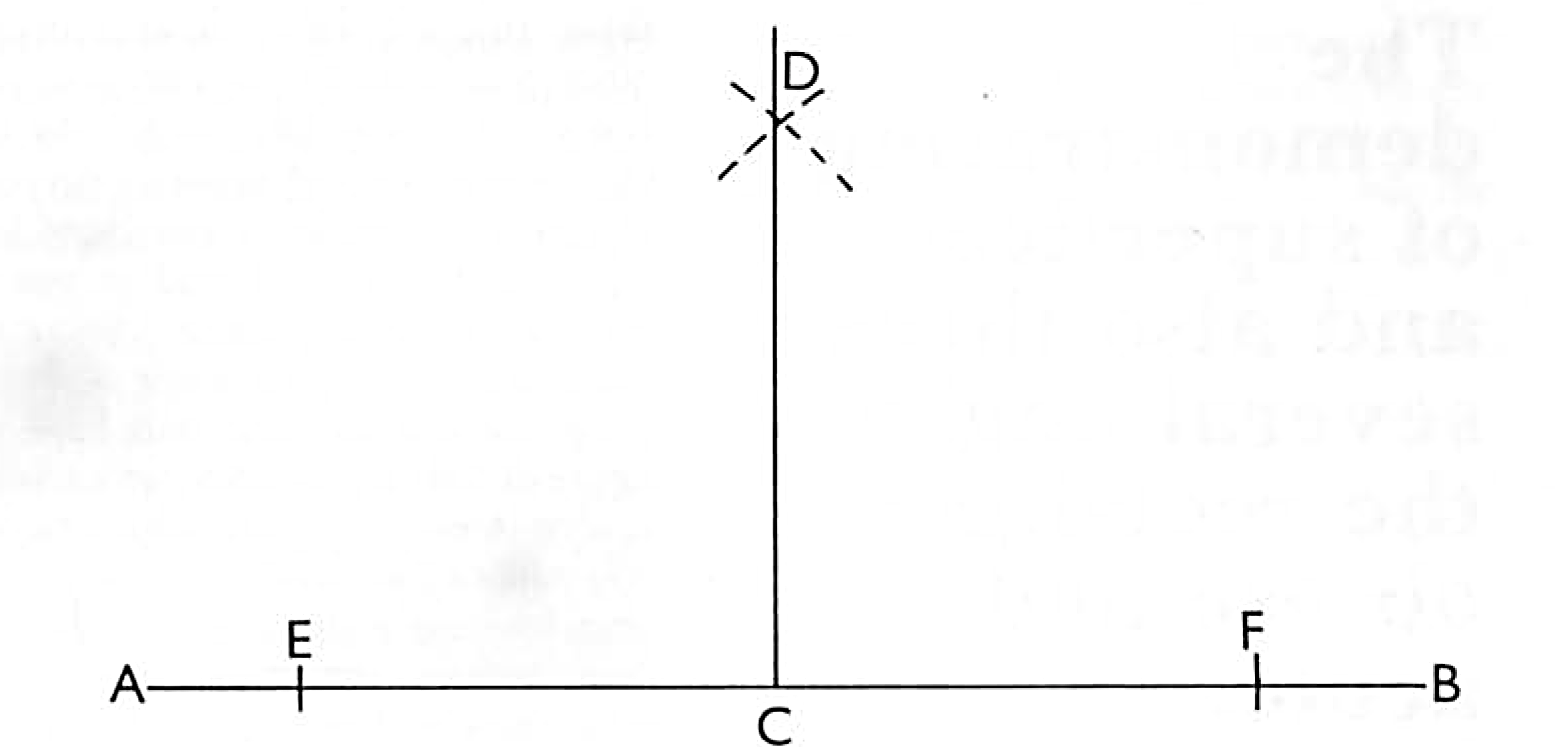
To Raise or let fall a perpendicular upon any right line given. Let AB be a line given and let C be a point there.in, whereon I would raise a perpendicular. Open your compasses to any convenient distance and, setting one foot in the point C, with the other leg mark on either side thereof the equal distances as CE and CF.

Then, opening your compasses to a convenient distance wider than the former, setting one foot in the points E and F, and strike two arc lines crossing each other as in D, from whence draw the line DC, which is a perpendicular to AB, or as we call it, a square line to the line AB.

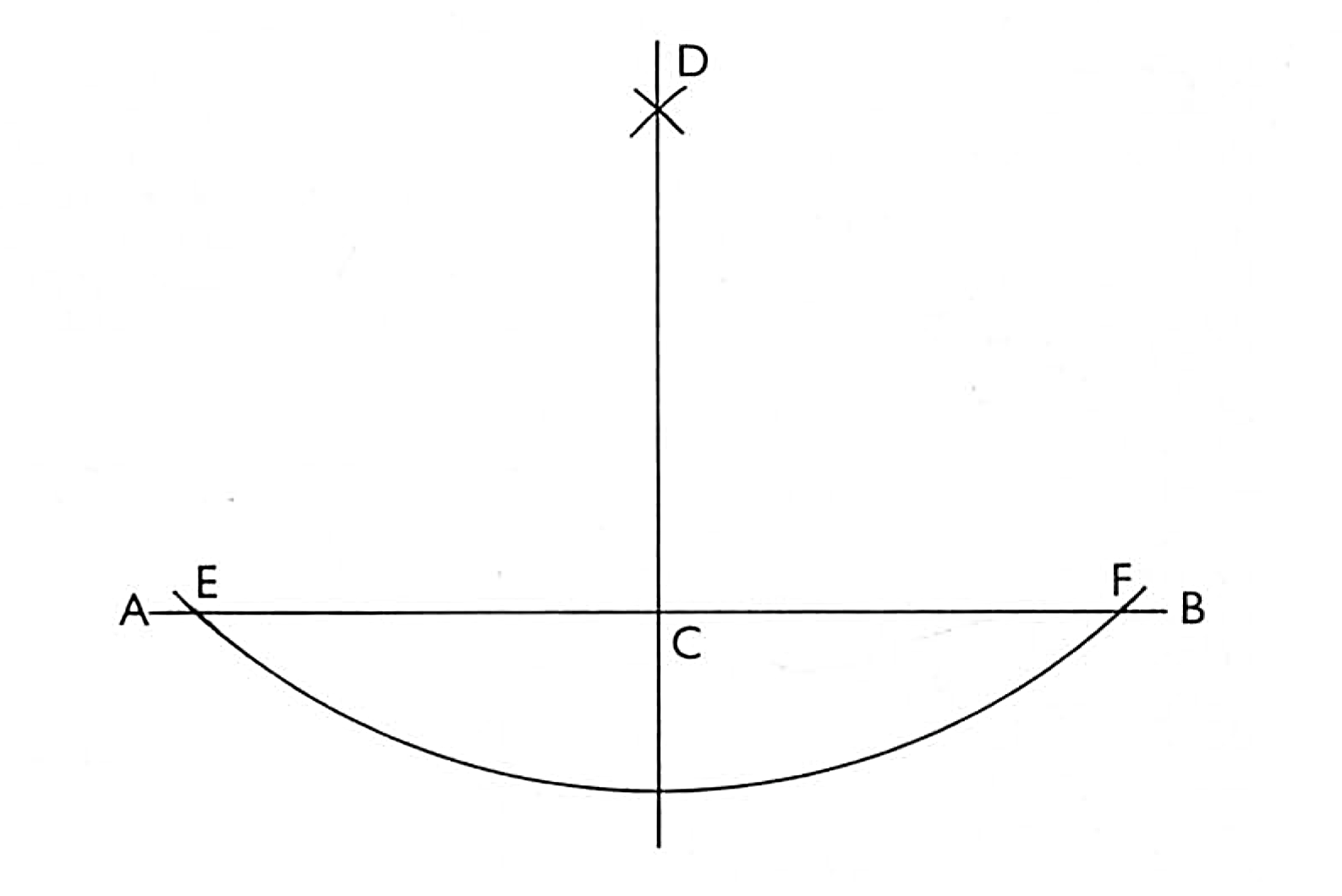
To let fall a perpendicular from a point assigned to a line given, as for example let the point given be D, from which I would let fall a perpendicular, and let the line whereon it should fall be AB. Open your compasses to any convenient distance, and, setting one foot in the point D, make an arc or piece of a circle with the other foot until it cut the line AB twice, that is at E and F, then find middle between these two intersections, and from that middle draw a line to C from the point D, which is the point given, and that line shall be perpendicular or plumb from the point D unto the line AB as was required to be done, and will be often in use for the work we are to proceed in building, and therefore requires your memory of this easy but useful demonstration.

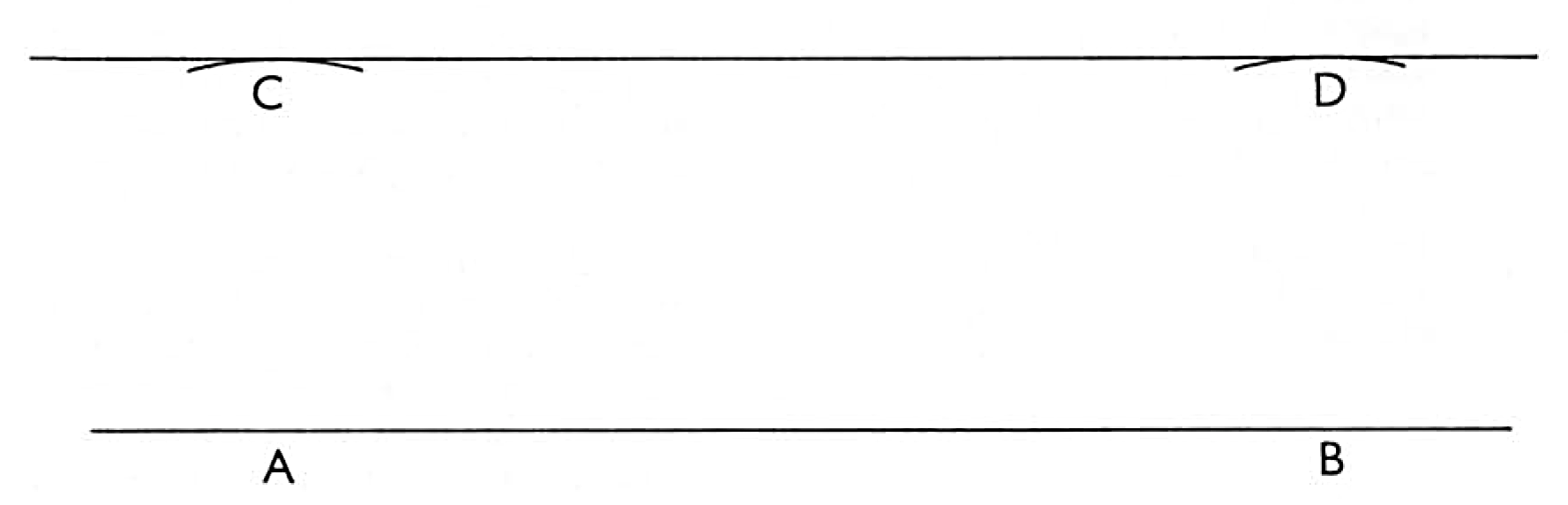
To a line given to draw a parallel line at any distance required. Supposing you now well understand a line straight or circular, and also a perpendicular, you shall be instructed in the drawing of any lines parallel one to the other, as for example I would strike a line parallel to

the line AB. Open your compasses to any convenient distance. Set one leg at A, and with the other strike an arc at C.

Again set your compasses, keeping the same distance, at B. Strike an arc as before. Having so done, strike a line at the extreme of both arcs and it will be the line C and D, parallel to the line AB, both lines being of equal distance from one another in every part, which was required to be done. In understanding this method, all parallels are of like nature, let them be perpendiculars or bases. The work is all wrought as by this, above said.