The demonstrating of superfices, and also three several angles, the rectangle, obtuse and acute

To describe a superfice. Having as I conceive made you perfect in the knowledge of lines, it remains to instruct you in the uses thereof, which being applied makes a superficies of several sorts, as for example strike a straight line AB, whereon raise a perpendicular at A to C.

Open your compasses at such distance as you please, setting one leg at B. Strike an are parallel to the line AB, which is E. Having so done, keep the same distance, setting one leg at A. Strike an arc from A to C, then strike the line CE, which makes the depth of this figure, and for the length as you please, doing as you have been taught. By another parallel make the line BE from the line AC, and thus you have a figure of four sides, which being only length and breadth without depth is called a superficies, or plane, contained under four sides.

There are many various shapes as the lines are applied, and therefore I shall show you others, for example suppose a straight line AB whereon is raised a perpendicular line AC. Strike a third line from C to B, and the figure so prescribed is a three sided figure or superficies, and is called a right angle 2 for shape, which having added unto the same quantity makes a square. And then is the line CB a diagonal line, and thus may you treat as many shapes as may serve your turn until your work ends.

Before I proceed to tell you what an angle is, I shall give you a demonstration of a square figure which is four equal sides, the one side not exceeding the other, and is of all things necessary to be known. The way of raising is by drawing a line as AB and raising a perpendicular on each end at A and B, of length equal to the line AB, and as you have been taught set one leg in A and strike a small arc, doing the same at B, then strike the line EF, and thus have you a figure of four equal sides, which is a due square in every way.

In which figure, if you strike a line from corner to corner, it contains two right angles, if from the four corners the lines crossing each other there will be contained four angles, so that this figure is called a quadrangle as well as a square, which was required to be shown, as is more plain in the figure ABCD.

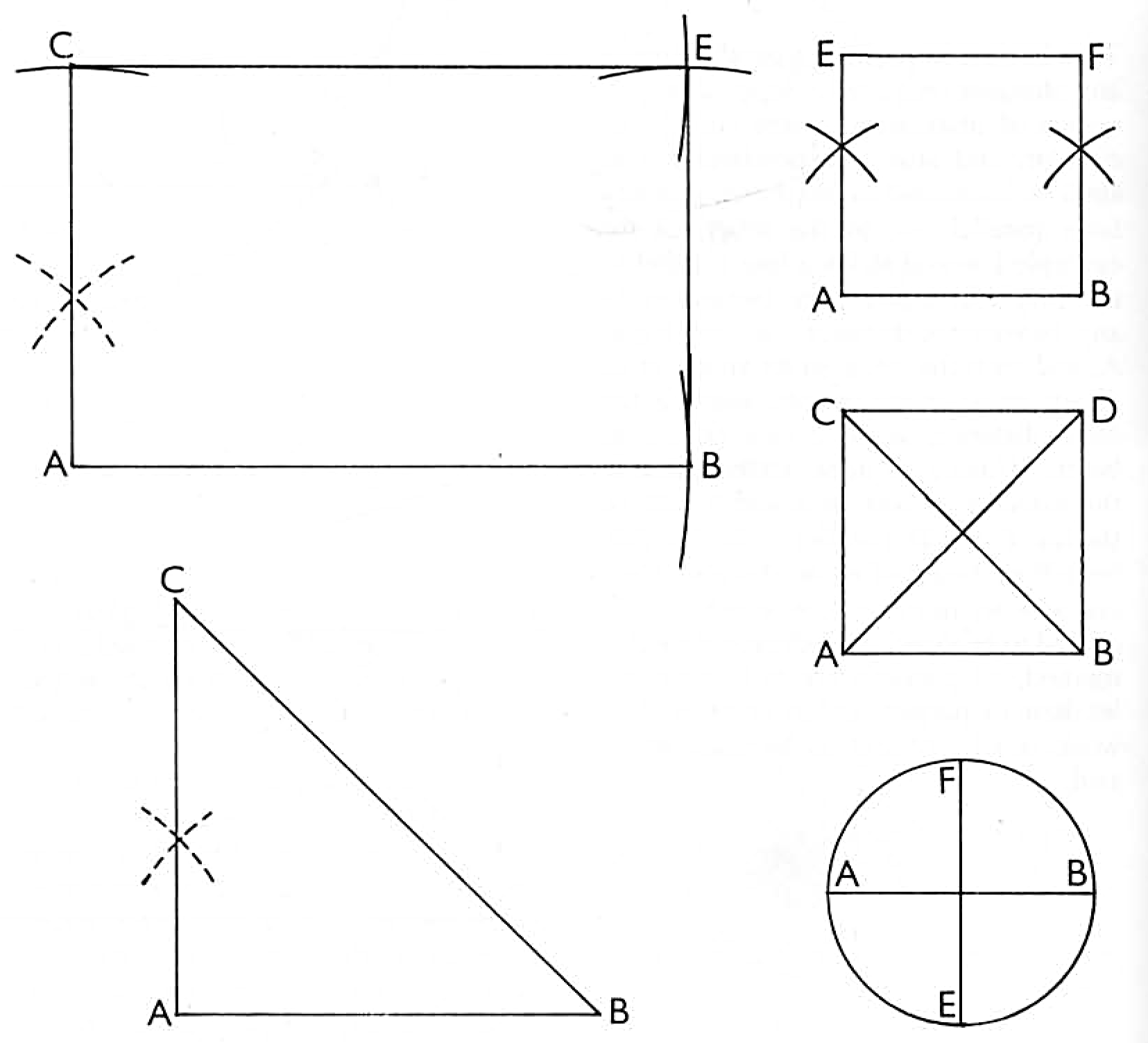
This square figure divides a circle into four equal parts. As for example, draw a circle, wherein draw a line crossing the centre and it will divide the circle into two equal parts, as you see the line AB divides the circle equal. Then raise a perpendicular on the centre and strike a line from E to F and it will divide the circle into four equal parts. Each part is commonly called a quadrant, which was required to be known.

To describe an angle. There be several sorts of angles, but none so useful for our work in hand as those which shall be laid down, namely rectangles, obtuse angles, and acute. Nor is there anything more beneficial than the ground of these unto the young artist. Therefore I will set them down in their several shapes from which they receive their names, beginning with the right angle.

Suppose a line for your base is AB. Raise a perpendicular from C to D. Having so done, your angle is made by the perpendicular or plumb line at the point C, and hath his name of right or rectangle, from its upright line which divides a circle into four equal parts, for whatsoever is perpendicular unto any line divides each side of the line alike, nor is an angle any more than two lines meeting together, and is distinguished by dividing the circle equal or unequal as shall be shown. This is therefore a right angle.

The next shall be an obtuse The obtuse angle is greater than the right angle by so much as it extends itself from the perpendicular line you last made in your rectangle. As for example, draw a line as AB, raising a perpendicular at C to D. Having so done, open your compasses at any distance not exceeding the length of your lines from D to E, then draw a line from E to C, and then have you an obtuse angle ACE, forasmuch as the angle ACE is wider than the rectangle ACD, and contains the angle DCE more than the angle ACD.

Which was required to be done, and thus you see that the obtuse angle is all ways greater than a rectangle. It remains to show an acute angle as in the next shall be described.

The description of an acute angle. An acute angle is less than the rector obtuse angle. As for example, draw a line as AB, whereon raise a perpendicular CD. Having so done, open your com-passes as in your last work, setting one leg in D to E, then draw the line from E to C. It makes an acute angle BCE, and is less than the rectangle ACD by the angle DCE, so that by this you may plainly perceive the nature of the three angles apart.

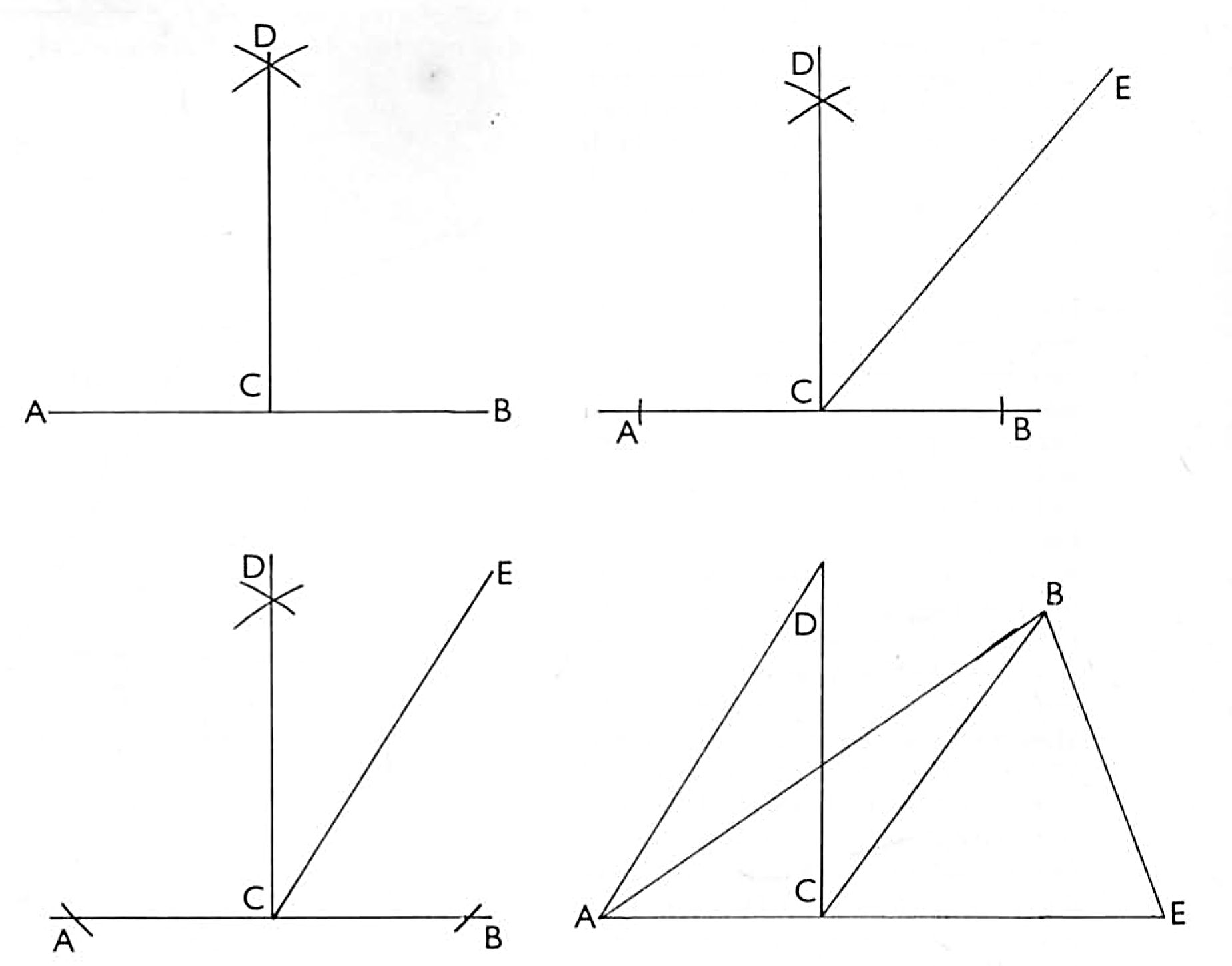
The obtuse biggest, the acute the least, and the rectangle the mean. So that there needs no more concerning the knowledge of these, only, by the way, it is not amiss to show you that the several angles in one figure, as you see here demonstrated by the lines ACD is a right angle, as you have been taught, the lines ACB an obtuse angle, the greatest, and the lines BCE an acute angle or least, and thus have you the definition of these three angles, and the way of prescribing them by geometry, which you must know ere you pass unto our works, which will be perceived in its due order. Hoping you well understand now the three several angles, do pass unto the making of a scale.