The reconciling of several sweeps demonstrated

There is nothing more advantageous in the whole work of a shipwright than the well understanding of the several lines on this page, the use of which is worth your knowledge, and therefore I have chose to lay it down here, rather than hereafter, by reason it is a work which you cannot pass by without keeping you in ignorance, which I am not willing to do, being contrary to my end.

And intended this work to distinguish the several lines which you find in every page, some having the names of rising lines, some called narrowing lines, some toptimber lines, which may be shown on the plate at once, but not so obvious as you shall see here, one or two examples

wrought, by which you may see all the rest more plainer. And we will suppose a line struck at 120 feet in length from A to B, where we will suppose a perpendicular is raised at C, 80 feet from A, and we will conceive this to be a keel line of that length, raising another perpendicular at A to D, 18 feet, by arithmetic.

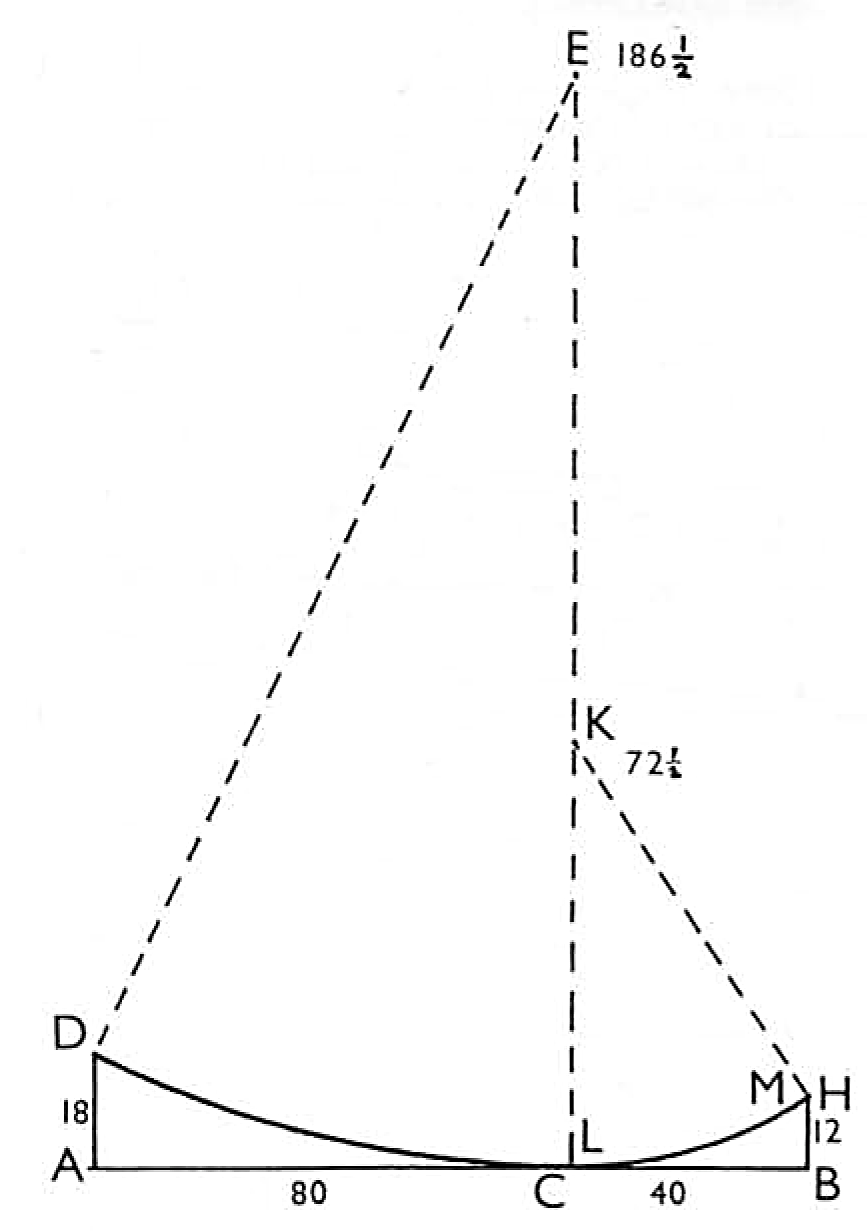
Work thus. Multiply 80 by 80, the basis - 6400, and divide this 6400 by 18, the line AD 18 feet - 355. To this 355 add 18, the line AD- 373. The half of this 373 is the centre required, which is 186 feet and a half, and if you set one leg of your compasses in E it will sweep the line FGD. Having done with that line, I would know the centre of the other part of the line from C to B, which is 40 feet or parts of a foot, and the line BH, 12 feet. I work as above, multiplying 40 by 40, the basis - 1600. This product 1600 I divide by the line BH, 12 feet, as thus- 133. Unto this 133 I add the line BH, 12 feet, as thus- 145. This 145 feet or parts of a foot I divide by 2 thus – 72 1/2. This 72 1/2 is the true radius, which, if you set one leg of your compasses in K, it will sweep the line LM, and thus have you these two centres reconciled at C, by which you may see the great harmony each part bears with the other, for had you not this knowledge your bow would deceive you, which now you correct not, only that but all other errors.

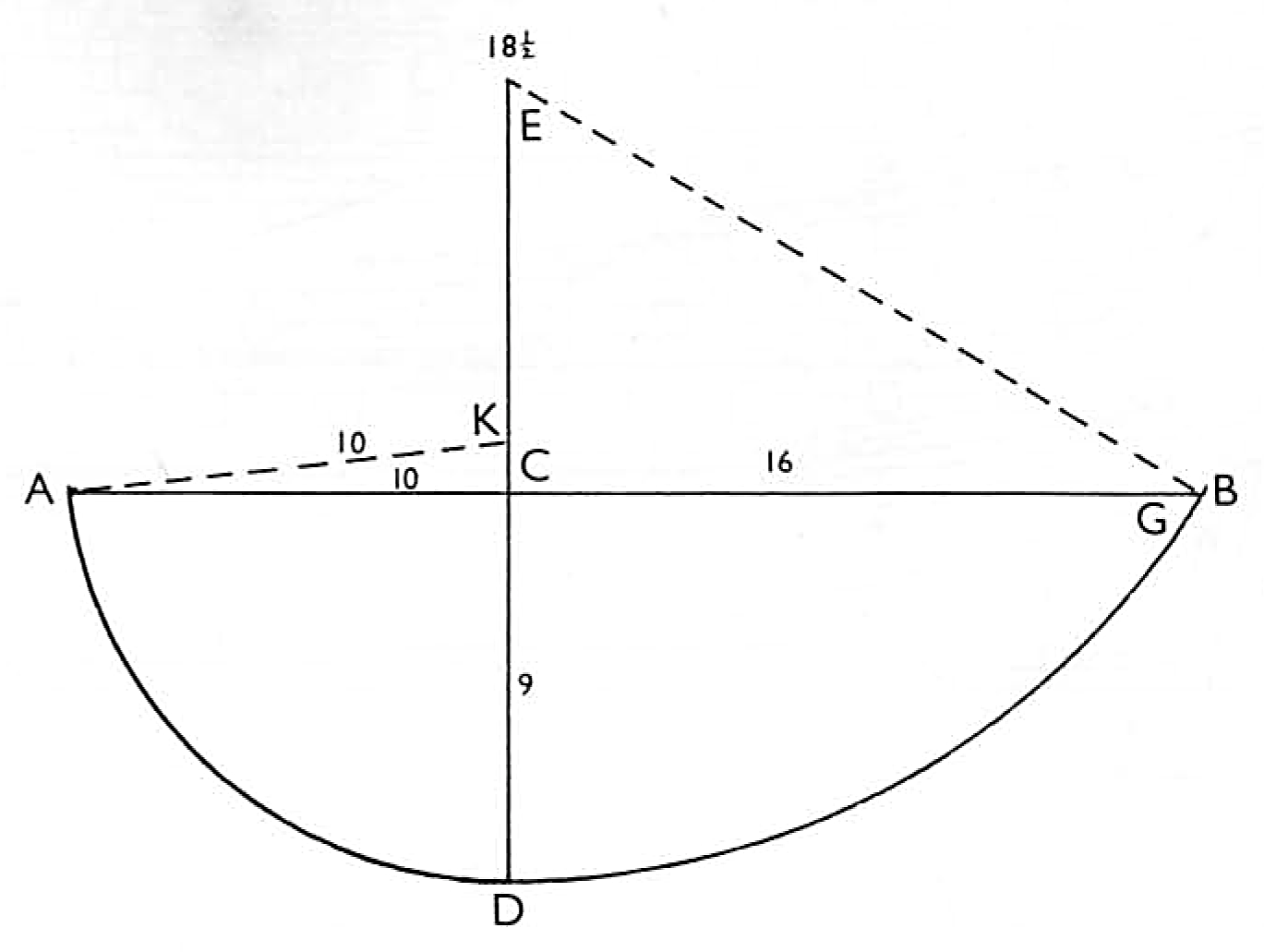
Before you cease in this work, I will show you one instance more. Supposing it an upper rail of a head, which we will suppose is 26 feet by a straight line, as you see the line AB, 26 feet or parts. On this line we let fall a perpendicular from C to D, 9 feet or parts, which is 16 feet from C to B, then I work thus. Multiply 16 by 16 as thus- 256. This 256 divide by the line CD as thus- 28. Unto this 28 I add the line CD, which is 9, as thus - 37. Half of this 37 is the centre required, 18 1/2, which if you set one leg of your compasses in E shall strike the line CD. Now that part is done, the other is wrought by the same method, as suppose from A to C, 10 feet, then I say 10 times 10 is 100, and divide it by the perpendicular 9 as thus - 11. Unto this 11 add 9 as thus - 20. The half of this is the centre, which if you set one leg of your compasses in K it will strike the line from D to A, which I hope you now sufficiently understand, not that I assign these lines to any use, but suppose they were of these dimensions, for if they be thus or of any other, this method shall them good in every proposition.

In the last plate we came from, I did entrust you in the way of working any lines by arithmetic, but as yet we have not taken any notice how to find the true rising of any timbers after the lines are found out, or the narrowing also, which I will here hint, on proposition to find out any timber's rising or narrowing without any bow or draught, which suppose to do thus. You see the line AB, which is 80 feet, which we will conceive the length of the keel from the midships to the stern post, and the line AC, the perpendicular of the post or the like, 22 feet. I then work as before taught, multiplying 80 by 80 which is 6400.

This I divide by 22, the line AC. The quotient is 290 20/22 . Unto this I add 22, the line AC, and it is 312 20/22. The half of this 312 is the centre required, which is 156 feet, which if you set one leg of your compasses at E it will strike the chord or line from B to C. Now you have the basis AB, 80, and the perpendicular AC, 22, and the third side BE, 156, I do demand how much the timber shall rise at K, being from B 60 feet, which I work thus, multiplying the side BE, which is

156, unto itself squarely, and it is 24336. Having so done, I multiply my side BK, 60, unto itself as the other, and it will be 3600. This lesser sum 3600 I subtract out of the greater, and there remains 20736. Having done this, I extract it by the square root, as thus - 144. This root of 144 I subtract out of the line BE, 156, and there remains 12. This 12, being set off from K to L, is the just rising of the timber which I desired should stand in that place, K .

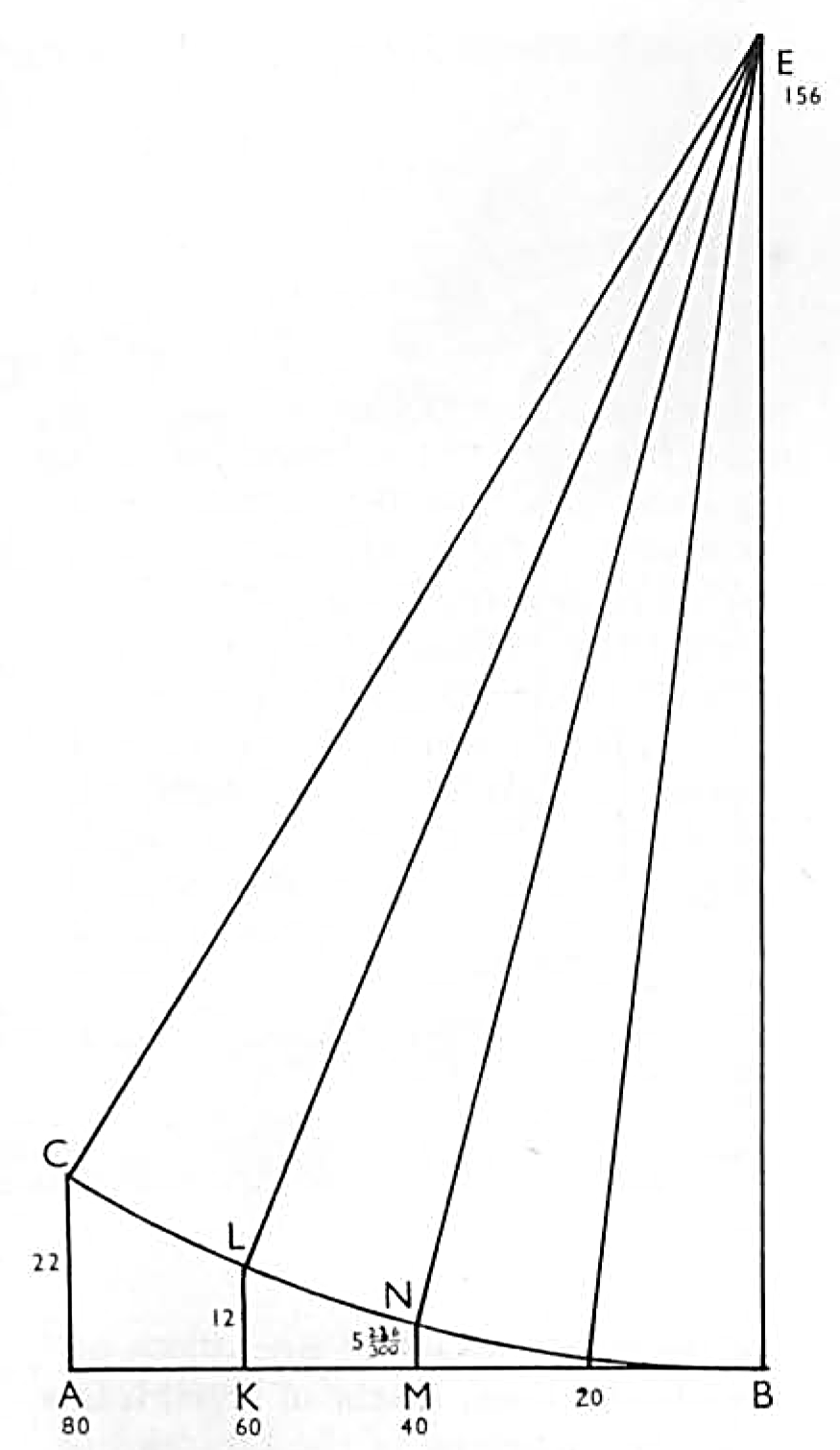
This is worth your observation, which, if you carry in mind, it worketh all the rest. Yet I will show you one example more, as suppose I would know the rising of the timber at M, which is from B 40 feet. Then I say as before. Multiply the side BE, 156, unto itself, and it yields 24336. Having done so, multiply the side MB, which is 40 feet, unto itself and it will be 1600. This 1600 subtract out of the above 24336, and there remains 22736, out of which you must extract the square root as thus – 150 236/300 . This 150 with its fraction you subtract out of the side BE, 156, and there remains 5 236/300, which is the true rising from M to N . The fraction in many places is omitted to keep the memory unburdened, and thus have you two examples. The rest is the same work, and therefore I say no more, but leave it to your own industry as you find cause.