By a plain scale to measure round timber and cast up wages with the use of numbers

To measure round timber geometrically. In the last chapters you were shown the several ways of measuring board and timber of any dimensions. In this you shall be instructed how to measure round timber, called girt measure, as suppose a piece of round timber whose diameter is 16 inches, and whose length is 15 feet. I desire to know the content of square feet of such a piece, but by the way, pray remember that I here procure you a centre of every round piece, which is 13 inches and near f of an inch to work, by reason it would be too much work, and perhaps the young artist not fit to receive it, as shall be shown hereafter.

So work thus, as in your former chapter, remembering that the centre of every round piece is 13 inches and very near 4/8 ths, as in square timber your centre is 12 inches. Proceed thus. Strike two lines like an angle, and let them be ABC, meeting at B. Having so done, take from your scale 13 inches and near 4/8 ths, and set one leg at B, extending the other to D. Then take your length, which is 15 feet, and set it from B to E.

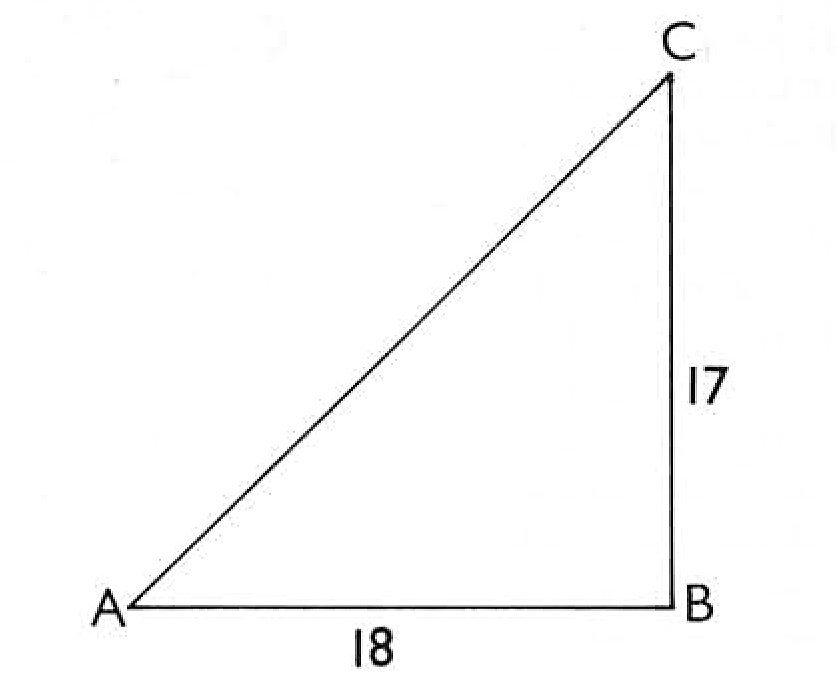
Then strike the line DE. Having so done, take your breadth, 16 inches, and set it from B to G, and strike a line parallel to the line DE, which will be the line GF, which will prove from F to B

24t feet, which is the resolution of the question. In like manner is all round timber measured.

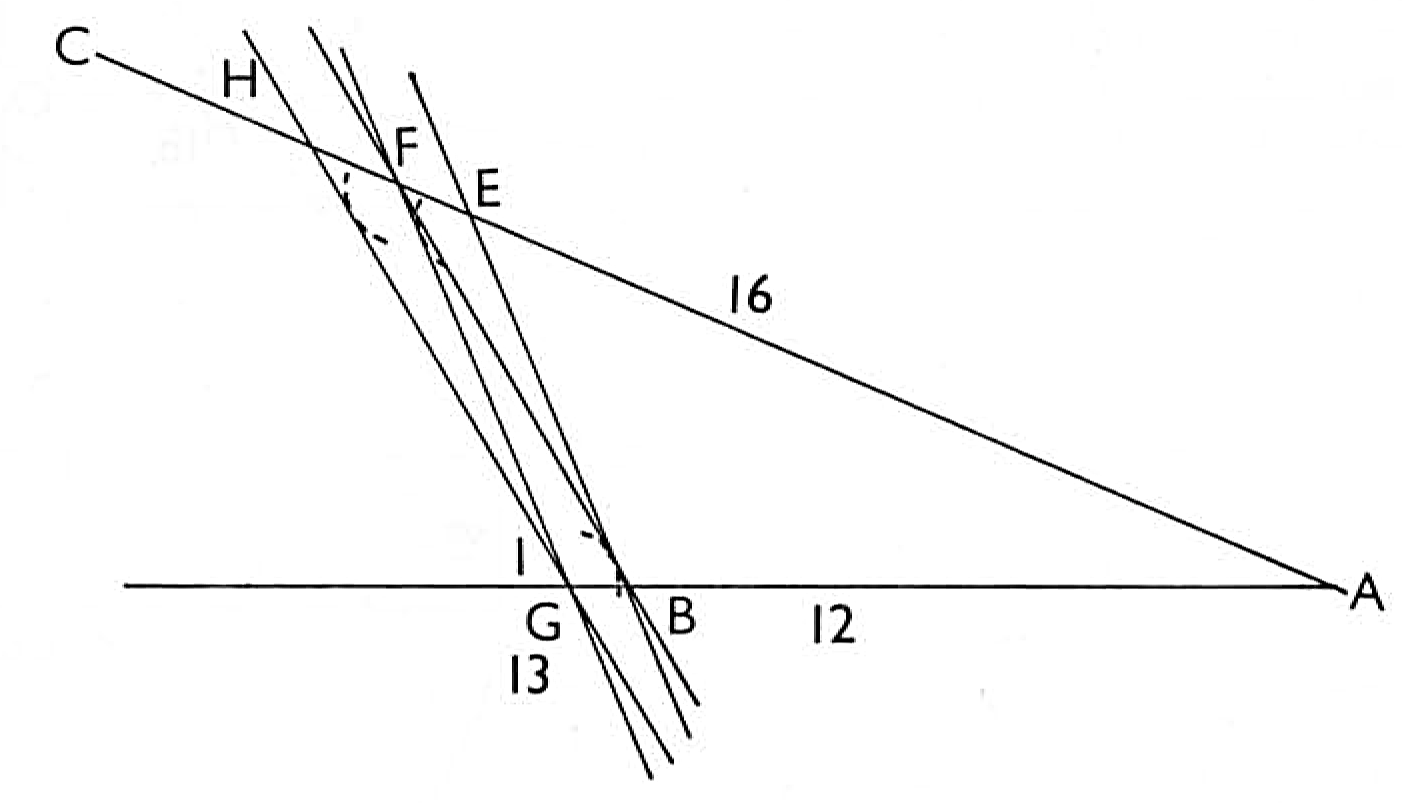
To measure any piece by geometry whose end is a triangle or a three sided figure. I would know the timber in this piece, being 16 feet long and 18 inches basis, and 17 in perpendicular. This work differs nothing from the former, only to find the square of the sides, which is always the one half the base and the whole perpendicular, as suppose the line AB, the base 18 inches, and BC the perpendicular, 17 inches.

The square is 13 inches, by taking the one half of the line AB, which is 9, and the whole line BC, being 17, added together makes 26, the half of which is 13. Having now found the square of your three sided figure ABC, work as before, striking two lines meeting at A, then take 12, which is always a side of a foot square, and set it from A to B. Having so done, take your length, which is 16 feet, and set it from A to E. Then strike the line EA. Having so done, take your breadth or square, which is 13, and set it from A to G. Then strike the line G F parallel to BE, and thus have you one side.

Now, to find the other side of the timber, having thickness as well as breadth, strike a diagonal line from F to B. Having so done, set one leg at G, taking the distance from G until it cuts the line FB. Having so done, strike a line parallel to the line FB, which will be the line HI, whose distance from H to B will be 18t feet of timber in that piece. And thus much shall suffice. All timber by this application will be truly measured.

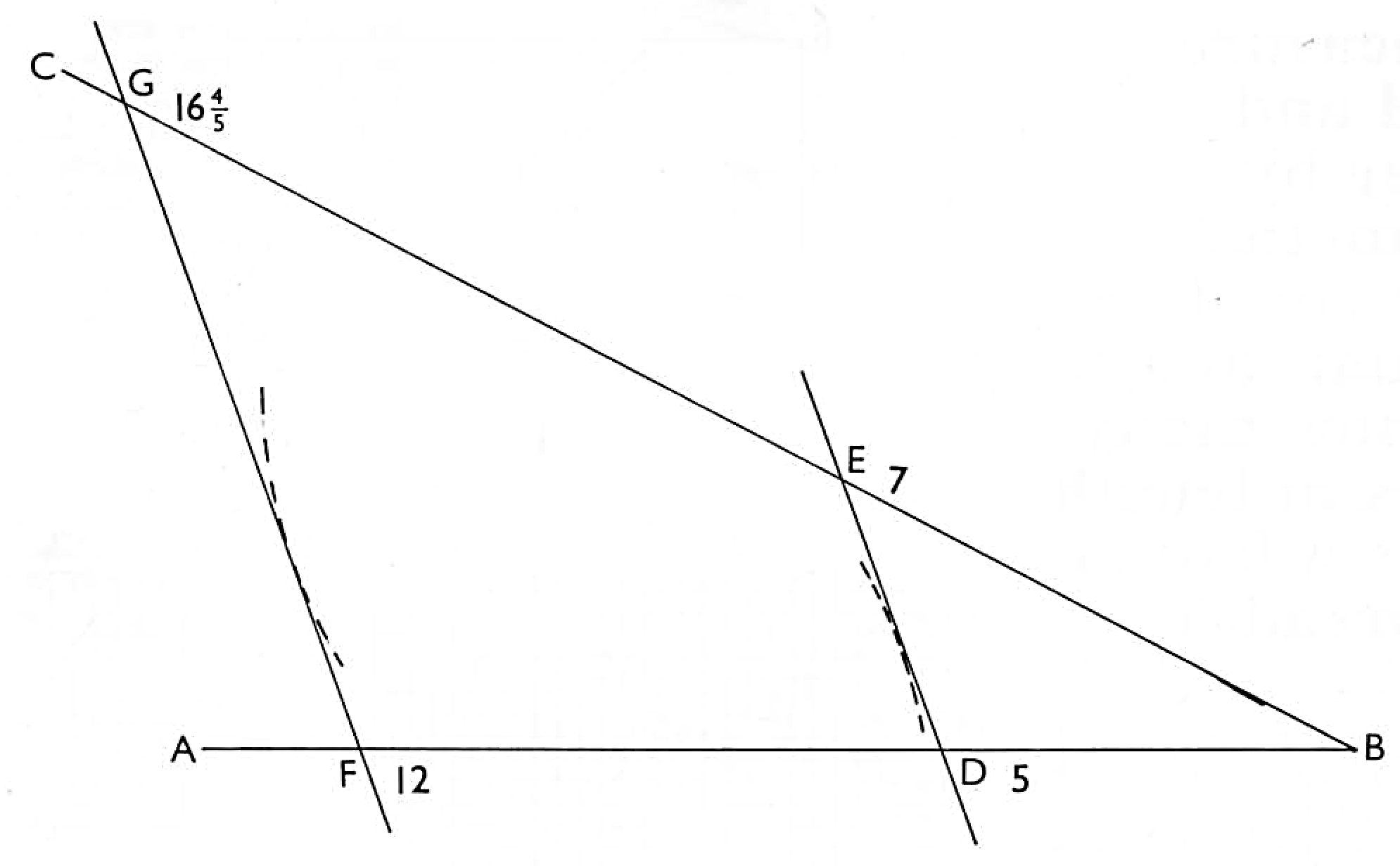
To cast up wages by geometry, or any sums of money whatsoever. Suppose that five men earn seven pounds. What shall twelve men earn? Work thus. Strike at adventure two lines, as suppose

the lines ABC, meeting like an angle at B. Then take from your scale of equal parts five, and set it from B to D. Having so done, take seven from your scale and set it from B to E. Then strike the line DE. Having thus done, take from your scale twelve, which signifies men, and set it from B to F. Having so done, strike a line parallel to DE, which will be the line FG. And now will it prove from G to B 16·t, which is 16 pounds 16 shillings, which is the desired question.

In doing this, and observing well its reason, there will be no more need of propounding any more questions, it being very plain that, five men earning 7 pounds, that twelve men will earn 16f,

by the rule of proportion. And in like manner is every question wrought, having two numbers to find a third, and having three numbers given to find a fourth, in continual proportion. And

therefore, considering my promise, I do pass away from the rules of geometry, excepting the instructing you how to find the centre to any segment or part of a chord whatsoever, which follows my next proposition.

To find the centre of any segment geometrically. Suppose I would find the centre of any segment or piece of a circle, as ABC. First take a point at pleasure with most convenience in the arc ABC, as at B. Now on the point B, at any convenient distance, describe a circle EFGHIK. Which being done, remove your compasses to the point E, where the circle crosseth the arc line given. Now, one foot being set in the point E, and at the same distance as before, cross the circle twice, as at F and K, and with the same distance at the point H cross the said circle twice more, as in G and I, and lastly, by these intersectings or crossings draw the lines FK and GI, until they meet or cross each other in the point L, which shall be the centre required.

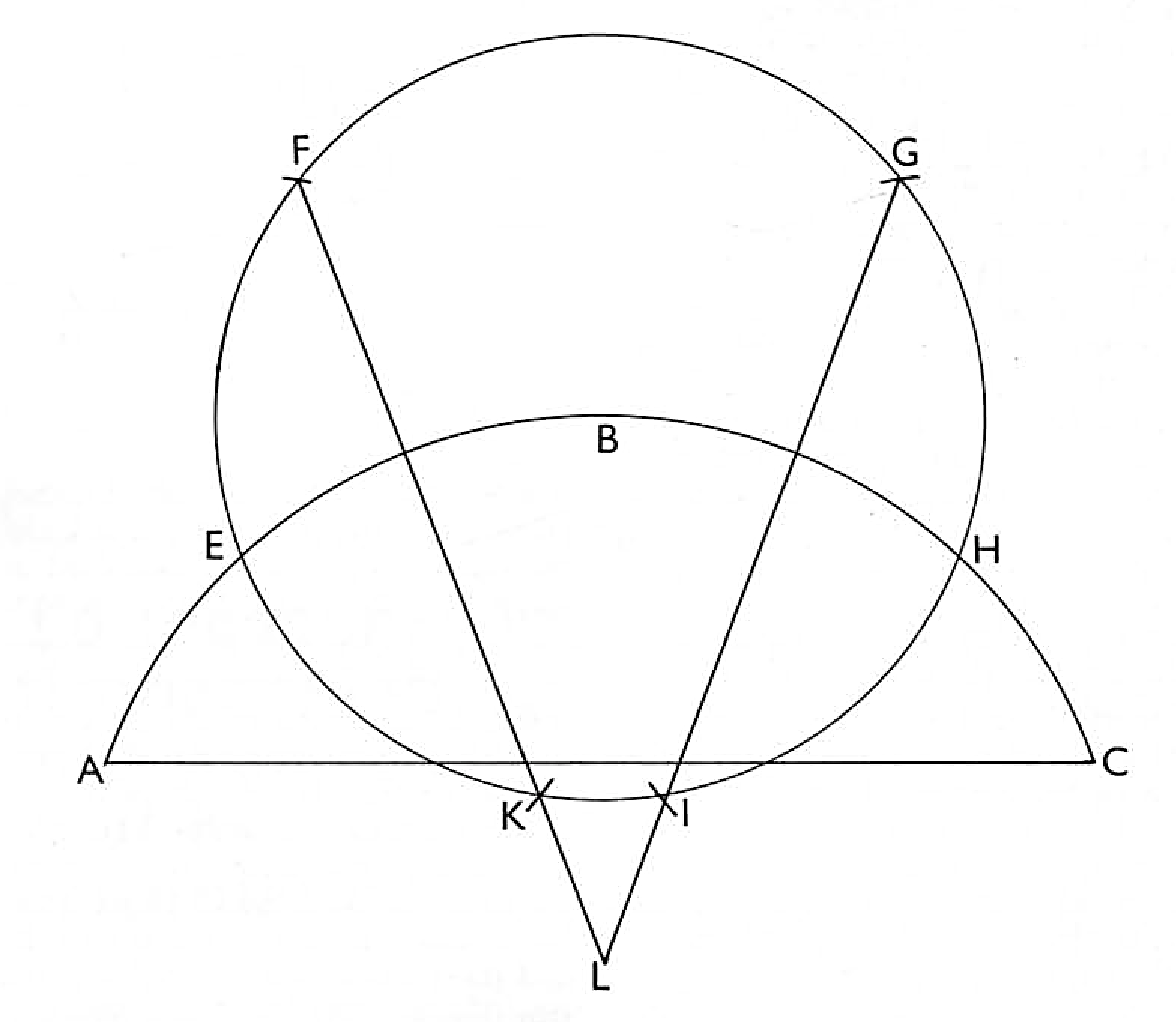
In like manner are all centres to be found out, and therefore shall I trouble you with no more geometrical questions, having laid down all that are useful for our purpose, which I hope the young artist now very well understands. And so shall I pass unto as many questions in arithmetic, that so both may be of use or compared on all occasions, for better manifestation of our whole work, as in the next shall be made plain.