Measuring the proportional length of a ship or logs apart

To measure the scantlings of ship's timbers by proportion, as suppose a ship of 400 tons, have a floor timber of 12 inches. I desire to know the bigness of a ship's floor timber of 800 tons. You must work thus. Cube the square of your floor timber, which is 12 inches, by saying 12 times 12 is 144, and 12 times 144 is 1728.

Having cubed your floor timber by your twice multiplying it, and that you would have the ship as big again, you multiply your 1728 by 2 and its product is 3456, which extract by the cube root, and your quotient will prove 15 81/401 inches, for the scantlings of a floor timber for a ship double to the former. But perhaps sometimes your proportion will not fall out double or treble so big as the former. If not, work thus, as suppose a ship's beam which is 12 inches square, whose burden is 500 tons. I would know the bigness of a ship's beam whose of 1050 tons. Work thus.

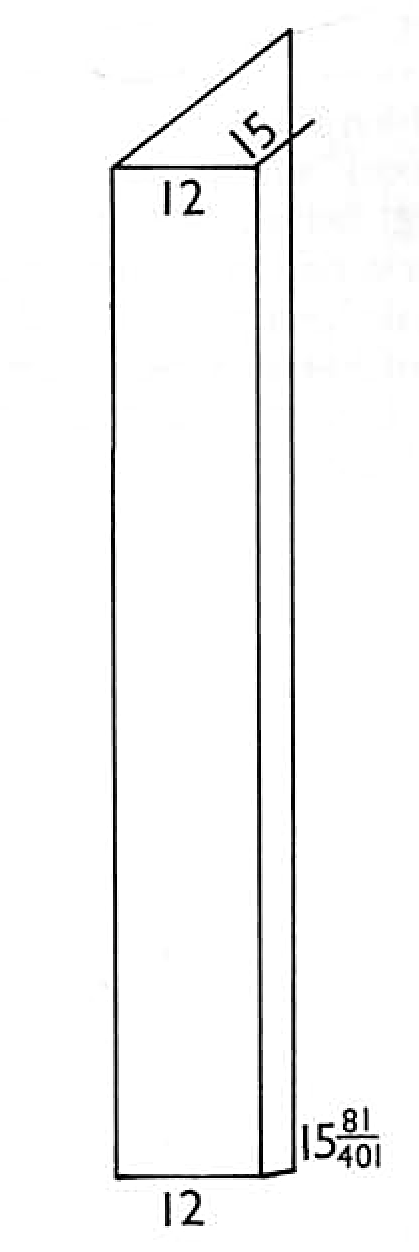
Cube your 12 inches as afore taught, saying 12 times 12 is 144, and 12 times 144 is 1728.

Having so done, say if 500 gives a cube of 1728, what shall 1050 give? Which by multiplying the second and third number together and it produceth 1814400, and divide by the first number

500 and your quotient will prove thus – 3628 400/525 . Out of this number 3628 extract the cube root, and your quotient will prove 15 253/261 inches. Having now showed you two ways of measuring the scantlings by proportion, I shall need say no more. You well understanding, this method will answer whatever you desire, nor can any proportion hold except it is wrought by this manner of labour.

To make ships oflike shapes and dimensions in every part, as suppose a ship's keel is 100 feet long whose burden is 544 tons. I desire to know the length of a ship's keel which is 978 tons. Work thus. Cube your 100 by saying 100 times 100 produceth 10000, and 100 times 10000 is 1000000. Having so done, work by the rule of three, saying if 544 gives 1000000, what shall 978 give?

Which, by multiplying the second number by the third, and divide by the first, your quotient will prove thus 1797794, out of which extract the cube root, and the quotient will prove 121 feet and something better, which is the true length for a keel of a ship which is 978 tons. Again, suppose the same ship's breadth, of S44 tons, be 31 feet. I would know the breadth of a ship of 978 tons. Work as before, cubing 31 by saying 31 times 31 is 961, and 31 times 961 is 29791. Having so done, work by the rule of three, saying if S44 gives 29791, what shall 978 give?

It will produce 53558, out of which extract the cube root, and your quotient will prove 37 feet and something better. So that by these two examples you may perceive how to proportion every part about the whole ship, making the great like unto the smaller, or the smaller as the great. But perhaps some will say this will produce shapes alike, but where are such shapes as are or may be called fit to be wrought, but my answer will be what my judgement leads me to believe, in another place, where the discourse is more suitable upon another subject of the like nature, and so pass to the next proposition.

To measure the tonnage of any ship whatsoever. In this matter I shall choose custom rather than truth, for ship's very full and broad will carry more than sharp or mean of like length, yet by reason sharp ships take up as much materials and labour, it is fit the builder should be paid the same rate for his works of equal length and breadth at the beam, although the owner of the ship desire her meaner, for some quality which best suits their occasion, or else I would show better, and more truer ways for measuring any burdens, as the ship would just carry by the true content of her body and her own weight.

But custom taking place, here shall be set down the usual rule, as suppose a ship 100 feet long by the keel, meaning from the back of the stern post to the touch of the stem, and 31 broad in the greatest breadth. The half breadth must stand for her depth to measure, by which is 1St. Work thus. Multiply your 100 feet length by 31 your breadth, and it produceth 3100. This 3100 multiply by 15 1/2, your depth, and it produceth 48050, which divide by 94.

Your quotient will prove 511 19/94 tons. And so much would the shipwright be paid for a ship of these dimensions. It's needless to set down any more examples. This work observed is the way of measuring any tonnage according to custom, as you have been told, not by any truth, which you shall discover when you come unto your other work, where we measure the whole ship's body and show the reason of her swimming or sinking by her own weight, and also her lading.

To know the content of gallons in any vessel round or square. Suppose a square vessel from A to B 20 inches, and from A to E 25 inches deep. I desire to know the content in wine gallons. Work thus. Multiply your breadth 20 inches, and it produceth 400. This 400 multiply by your depth 25 inches, and your product is 10000, which divide by 231 and your quotient will prove 45 105/231 gallons.

But if you would have it ale gallons let your divisor be 282. Again, suppose a butt whose diameter at the bung is 32 inches from A to B, and diameter at the head 30 inches from D to E, and length from I to K 50 inches. I desire to know the content in wine gallons. Work thus.

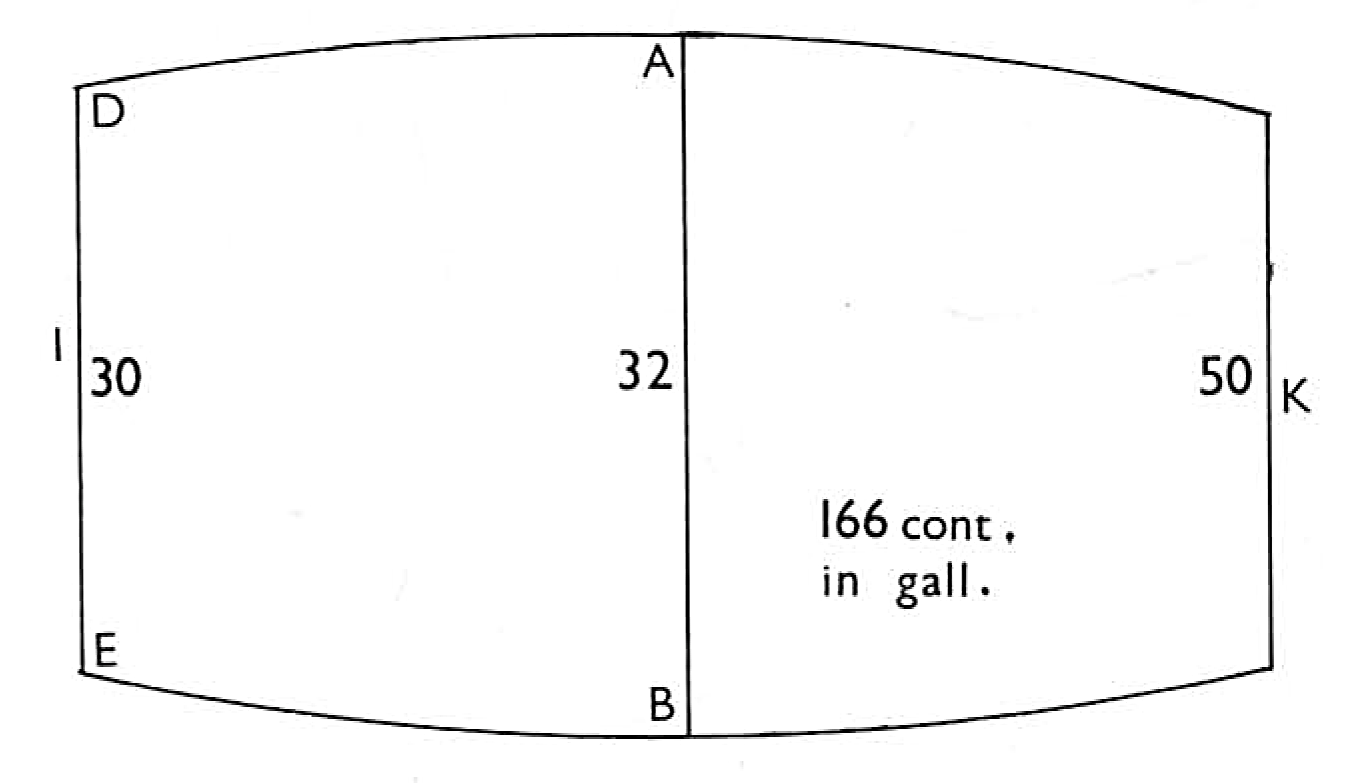
To find the mean diameter take two thirds of the bung which is 32, and it will be 21 3/4 , and one third of the diameter at the head, which is 30 inches, and it will be 10 inches. Having so done, add your 21 3/4 to 10 and it makes 31 3/4 inches, shall be the mean diameter between the bung and the head. Having found your diameter, square it, saying 31 3/4 by 31 3/4, and it yields 982, which multiply by 11 and it produceth 10802, and this 10802 divided by 14 your quotient will be 771, for your square diameter, which multiply by the length which was 50 inches and the product will be 38550, and divided by 231, the quotient is 166 gallons, the content of such a cask in wine measure. By these two vessels, square and round, you may with your own practice measure all others at your pleasure.