Atmospheric General Circulation and Climate
Chapter Summary. Geographic variation in the annual radiative balance at the top of the atmosphere drives the general circulation of the atmosphere and produces the major patterns of climate on Earth. The latitudinal gradient in net radiation results in an equator-to-pole temperature gradient. However, if only radiative processes determined temperatures, the tropics would be tens of degrees warmer than they actually are, and polar regions would be much colder than they actually are. Instead, the uneven geographic distribution of radiation produces winds, set in motion by differences in air pressure, that redistribute heat from the tropics to the poles. Winds are a balance of the pressure gradient force, Coriolis force, and friction acting simultaneously. These forces produce the general circulation of the atmosphere.
The continents alter this idealized circulation because landmasses heat and cool faster than oceans. In winter, when the landmasses of the Northern Hemisphere are colder than oceans, high pressure systems form over land while low pressure systems are most pronounced over oceans. The opposite pattern occurs in summer when continents are warmer than oceans. Oceans also influence climate by transporting heat poleward. Prominent ocean circulations are wind-driven surface currents and the density-driven thermohaline circulation. The general circulation of the atmosphere varies over the course of a year in response to seasonal changes in solar radiation. These seasonal changes in surface high and low pressure regions and atmospheric circulation drive seasonal changes in precipitation. Monsoons are one such prominent large-scale seasonal atmospheric circulation.
Air Pressure. Air pressure is the force exerted over a given area by the movement of air molecules. Air pressure is also a measure of the mass of air above a given point. Air pressure decreases with greater height above sea level because there are fewer air molecules, and less mass, with greater altitude.
The change in air pressure with height is described by the hydrostatic equation, which relates the upward force on a parcel of air due to the decrease in pressure with height to the downward force from gravity. This balance of forces is:

where dP is the change in pressure (pascal, 1 Pa = 1 N m-2 = 1 kg m-1 s-2), dz is change in height (m), p is the density of air (kg m-3), and g = 9.81 m s-2 is gravitational acceleration. The term pdz is the mass of air between heights z and z + dz. The downward force due to gravity is gpdz. This downward force is balanced by an upward force due to the decrease in pressure with height (-dP). Combining Eq. (5.1) with the ideal gas equation, from Eq. (3.12) and which provides an expression for density, gives:
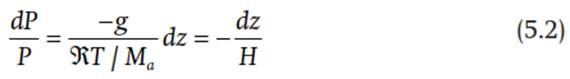
where H is the scale height. Integration of Eq. (5.2) gives the pressure at height z:

where Ps =1013.25 hectopascals (hPa, 1 hPa = 100 Pa = 1 millibar) is surface pressure at sea level (z = 0). An approximate value is H = 7600 m so that air pressure is 0.37Ps at an altitude of 7.6 km. The force of gravity holds most air molecules near the surface. With greater height in the atmosphere, the number of air molecules and pressure decrease.
Air pressure is related to the mass of air above a given point. This is evident by rearranging the terms in the hydrostatic equation to relate change in mass per unit area (dm, kg m-2) to change in pressure (dP):

At sea level, where the standard atmospheric pressure is 1013.25 hPa, a column of air covering one square meter of surface area and extending to the top of the atmosphere (i.e., to a pressure of 0 Pa) has mass:
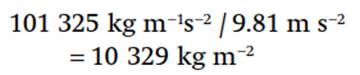
Multiplied by Earth’s surface area of about 510 million km2, the total mass of the atmosphere is about 5 x 1018 kg. Approximately fifty percent of the mass of the atmosphere is below a height of 5500 m.
The mass of an atmospheric constituent can be found from its volume mixing ratio. For example, the concentration of CO2 in the atmosphere is 390 parts per million by volume (Table 2.1). This is converted to total mass of carbon by multiplying this number by the mass of the atmosphere weighted by the relative mass of carbon atoms to the mass of air molecules. The molecular weight of carbon is 12 g mol-1 and the molecular weight of dry air is 28.97 g mol-1. This is equivalent to over 800 x 1015 g of carbon:
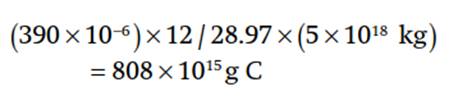
Date added: 2025-05-15; views: 469;
