Atmospheric Radiation. Solar Geometry

Solar Geometry. Diurnal and seasonal variation in climate arises from the geometry of Earth’s annual orbit around the Sun and its daily rotation on its axis. As Earth rotates over the course of a day, the Sun appears to sweep a broad arc through the sky. Two angles define the Sun’s position (Figure 4.1): its altitude above the horizon; and its bearing on the horizon, which is called the azimuth angle. A third angle, the zenith angle, is often used instead of altitude. Whereas altitude is the angular distance above the horizon, zenith angle is the angular distance from a line perpendicular to the surface. Altitude is zero at sunrise and sunset and is greatest at solar noon. At solar noon, the Sun is due south on the horizon in the Northern Hemisphere and is due north in the Southern Hemisphere. In the morning, the Sun is east of south; it is west of south in the afternoon.

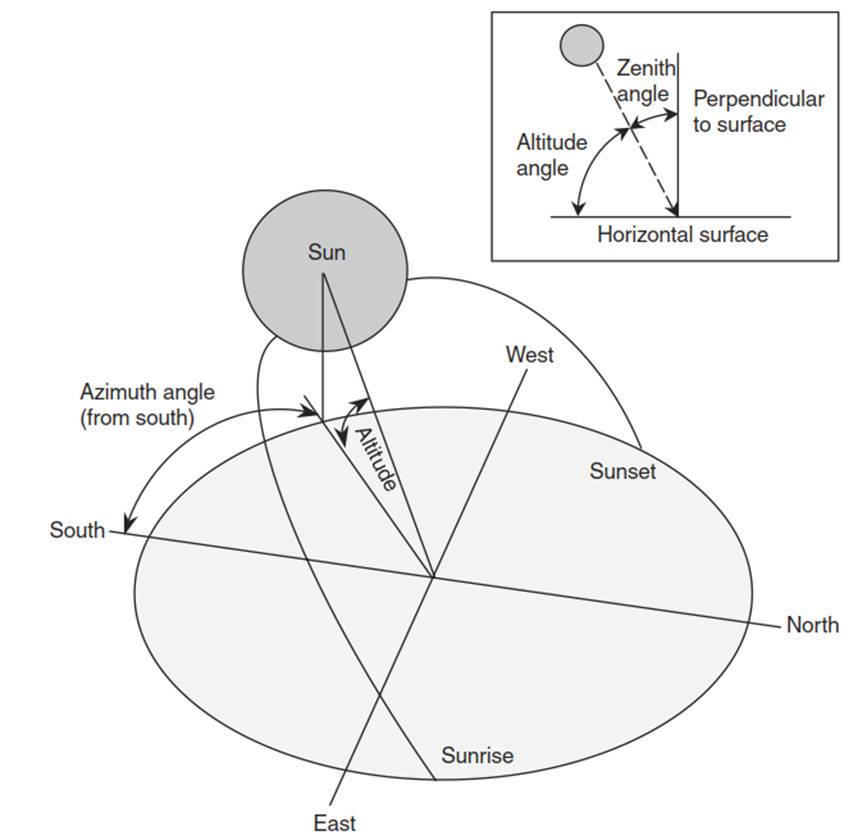
Fig. 4.1. Solar geometry illustrating azimuth, altitude, and zenith angles. here, azimuth angle is shown from south. The boxed inset shows the difference between the altitude and zenith angles

Zenith angle and altitude angle vary with latitude, time of year, and time of day:

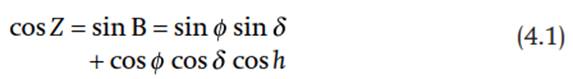
where Z is the zenith angle, В is the altitude angle, ф is latitude, δ is solar declination, and h is the solar hour angle. The hour angle measures time of day. Because Earth rotates on its axis 360° in 24 hours, one hour is equivalent to 15° of longitude, and the hour angle varies by 15° for each hour before or after solar noon. For example, the hour angle is 15° at 1100 hours and -15° at 1300 hours; it is 60° at 0800 hours and -60° at 1600 hours. At solar noon, when h = 0°, the zenith angle is at a minimum and the altitude angle is at a maximum. At this time, the zenith angle is equal to latitude minus declination, Z = ф-δ. This is the basis by which ancient mariners navigated the oceans. Measurement of the zenith angle when the Sun is highest in the sky combined with knowledge of the declination angle provides a precise determination of latitude. Solar noon occurs at 1200 hours local time only for the longitude that defines the time zone within which the observer is located. Solar noon occurs earlier in the day east of this longitude and later in the day west of this longitude.

The solar declination angle varies with the day of the year. Earth rotates over the course of a day on an axis tilted at an angle of 66.5° to an imaginary line connecting Earth and the Sun (Figure 4.2). This axis always points to the same location in space. Consequently, as Earth moves in its orbit around the Sun, the direction of tilt relative to the Sun varies. In boreal winter (austral summer), the Northern Hemisphere tilts away from the Sun while the Southern Hemisphere tilts towards the Sun. In boreal summer (austral winter), the Northern Hemisphere tilts towards the Sun while the Southern Hemisphere tilts away from the Sun. Seasonal changes in orientation towards or away from the Sun are seen in the declination angle. Declination is the angle between a line connecting the centers of the Sun and Earth and the plane of the equator (Figure 4.2). It is the latitude where the Sun is directly overhead at solar noon.

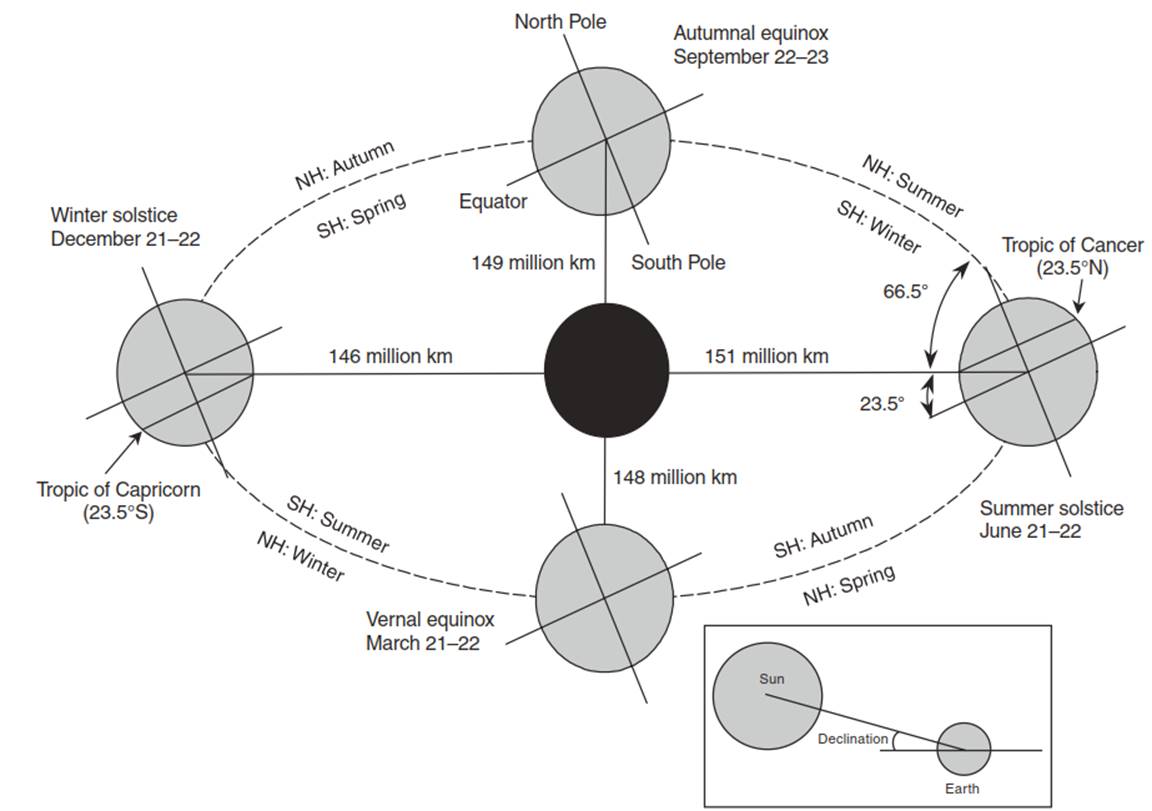
Fig. 4.2. The revolution of earth around the Sun and the resulting astronomical seasons. The boxed inset illustrates the declination angle. variation in the time of the solstices and equinoxes occurs because Earth’s 365¼ day orbit around the Sun is approximated by 365 days with an extra day every four years

Declination angle varies through the year (Figure 4.3). Four days of the year have special significance. On the winter solstice , which occurs on or about December 21, the declination angle is -23.5°. The Sun is directly overhead (i.e., has a zenith angle of zero) at noon at latitude 23.5° S. This latitude is the farthest point south of the equator where the Sun is directly overhead and is called the Tropic of Capricorn. On this day, which is the shortest day of the year in the Northern Hemisphere, regions north of latitude 66.5° N receive no solar radiation. This latitude defines the Arctic Circle. Daylight is continuous south of latitude 66.5° S. This latitude defines the Antarctic Circle. On the summer solstice, on or about June 21, the noon Sun is directly overhead at latitude 23.5° N. This latitude defines the Tropic of Cancer - the farthest point north of the equator where the Sun is directly overhead at noon. This day is the longest day of the year in the Northern Hemisphere. Daylight is continuous north of 66.5° N and is absent south of 66.5° S. On the equinoxes (on or about March 21 and September 22), the noon sun is directly overhead at the equator (i.e., the declination is zero). All latitudes receive 12 hours of light. The Sun rises due east at all latitudes on this day.

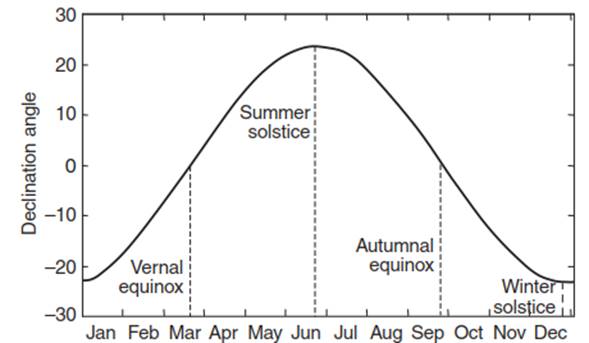
Fig. 4.3. Solar declination angle as a function of day of year

The azimuth of the Sun is the compass bearing of the Sun on the horizon (Figure 4.1). This direction is in the east in the morning and in the west after noon. The compass bearing at solar noon is either south or north depending on latitude. The azimuth angle (А_sun), measured as the angular distance from north, varies with time of year, time of day, and latitude:

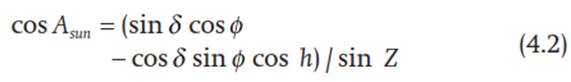
This formula gives the angular deviation, up to 180°, from north. It is more convenient to consider azimuth angles in terms of compass bearing. In the morning, when the Sun is east of north, the computed angle is also the compass bearing ranging from 0° (north) to 180° (south). In the afternoon, when the Sun is west of north, the compass bearing is equal to 360° minus the computed angle. Figure 4.4 illustrates the solar geometry at latitude 40° N for the winter and summer solstices. The Sun is higher in the sky and rises and sets further from south in summer than in winter.

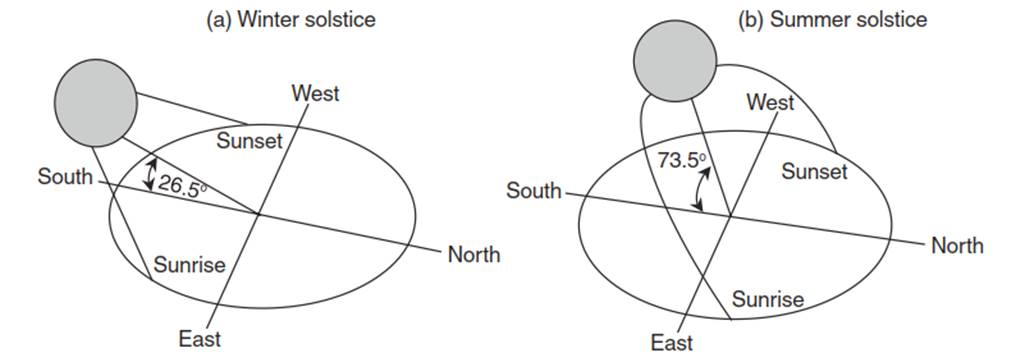
Fig. 4.4. Sun path diagram for latitude 40° N showing azimuth angles at sunrise and sunset and altitude angles at solar noon for (a) the winter solstice and (b) the summer solstice

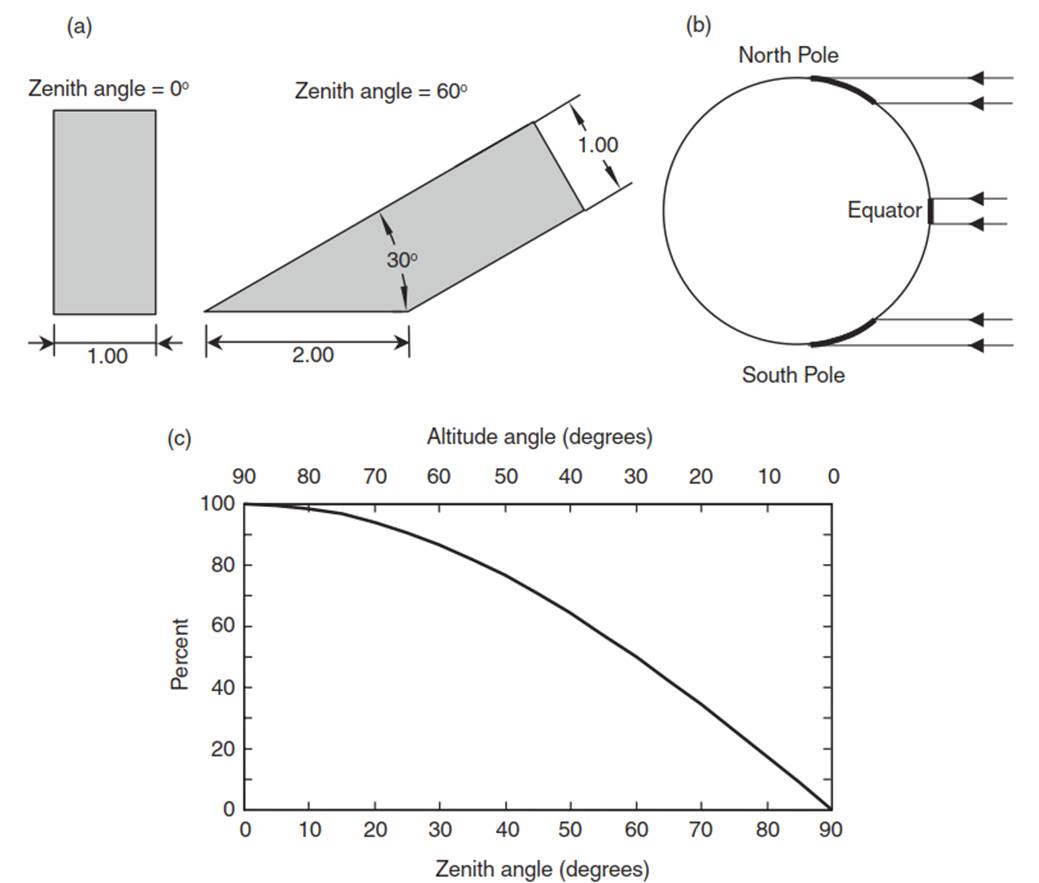
Fig. 4.5. The effect of zenith angle on solar radiation. (a) A beam of solar radiation with unit width spreads over twice as much surface area with a zenith angle of 60° than for a zenith angle of 0°. (b) Radiation spreads over a larger area at the poles than at the equator. (c) Radiation, as a percentage of perpendicular, in relation to zenith angle

The Sun’s position in the sky determines the intensity of radiation. A surface receives the most solar radiation when it is oriented perpendicular to the Sun’s rays (Figure 4.5) . At other angles, the Sun’s radiation spreads over a larger surface area leading to less radiation per unit area. For example, when the Sun is directly overhead a unit beam of radiation covers a unit surface area. When the zenith angle is 60° (i.e., the altitude angle is 30°), the same unit beam of radiation spreads over twice as much surface area; the energy per unit area decreases by one-half. The amount of radiation received on a horizontal surface (S_H) relative to that received on a surface perpendicular to the Sun’s rays (S_P) decreases with greater zenith angle:

A horizontal surface receives 87 percent of S_P when the zenith angle is 30°, 71 percent at 45°, and 50 percent at 60°.