From Joint Rotations to Limb Displacement

One of the interesting problems with joint rotations is that rotations about noncolinear axes in space do not commute. If you take a die and rotate it along two orthogonal axes in space, you will notice that the final orientation of the die depends on the order of the rotations.

This raises the question as to whether the orientation of limbs in joints with three degrees of freedom, such as the eyes, head, and shoulder, depends on previous rotations. The answer is they do not. The orientations of the eye, head, and upper arm are uniquely defined for each pointing direction of the arm or gaze direction.

This result is obtained by a specific reduction in degrees of freedom from three to two: all positions of the upper arm (both during movements and during stationary pointing) can be obtained by a rotation vector from a fixed reference position in such a way that all rotation vectors lie in a two-dimensional plane. Notice that this implies a reduction in degrees of freedom from three to two. To achieve this result, the angular velocity vectors that describe a movement have a fixed axis for each movement. The angular velocity rotation vectors do not fall in a plane, however, but they can have any orientation in 3D space, contrary to the rotation vectors, which describe the position of the eye, head, and arm.

To make straight movement trajectories with joint rotations requires a tight coordination in multiple joints. However, it also illustrates the necessity of biarticular muscles. Consider, for example, Fig. 6, which gives a schematic representation of a human arm that exerts an external force F. In Fig. 6, the lever arm relative to the external force F has the same orientation for the elbow and shoulder. Therefore, the torque in elbow and shoulder contributes to flexion. However, a movement in the direction of F requires elbow extension and shoulder flexion.

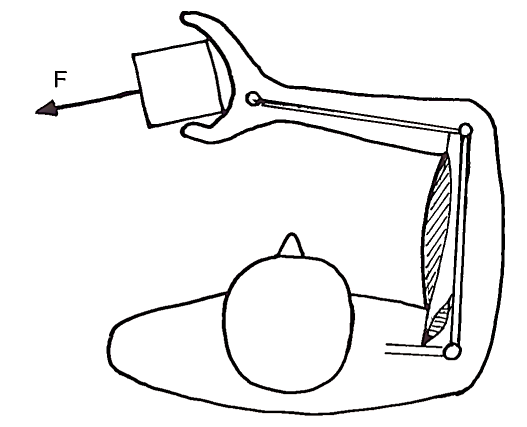
FIGURE 6. Schematic representation of the human arm. Notice that a movement in the direction F requires flexion of the shoulder and extension of the elbow. Also notice that a force in direction F requires a flexion torque in both elbow and shoulder. The most efficient way for making a movement in the direction F while exerting a force F is to activate the biarticular biceps muscle, assisted by additional activation of the monoarticular shoulder muscle to generate the required torque in the shoulder

Because of the opposite sign of torque T and change in joint angle 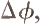the work is negative. If only monoarticular muscles would be available, they would dissipate work, rather than contribute positive work, as the monoarticular shoulder muscles do. This dissipation of energy, which is economically very unfavorable, can be partly relieved by using biarticular muscles. A biarticular muscle like m. biceps contributes to torque in both elbow and shoulder, but does not change its length as much as a monoarticular elbow muscle would, since the changes in elbow and shoulder angles give rise to opposite changes in length for m. biceps.

Similar apparent conflicts between torque and change in joint angle occur in daily motor acts such as walking, running, and cycling. Thanks to the presence of biarticular muscles, these motor acts can be performed with the efficiency and elegance that are observed in animal and humans.