RTT Strategies for the FPS

The complexity of the first subproblem can be reduced drastically by using modern RTT algorithms. Two main strategies are implemented in these algorithms:
- the shooting and bouncing of rays (SBR) strategy
- the solution of the inverse problem (SIP) strategy

The SBR strategy is illustrated in Fig. 5. This technique is based on shooting many rays in radial directions from the source. The path followed by each individual ray is obtained. This technique only considers the contribution from the reflections in the specular direction.

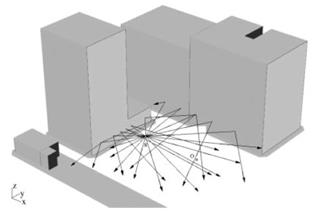
Figure 5. Example of SBR on a simple urban scene. Many rays are launched from the position of the source (S), and only the rays that pass close to the position of the observation point (O) are considered to illuminate that point

Therefore, applying this technique, when a ray hits a surface, its path is redirected following Snell’s law of reflection, and if the surface is penetrable, the law for transmission. The ray path is followed until it leaves the volume of the scene or when it has suffered a predetermined number of reflections. A ray is considered to contribute to the total illumination strength at a given observation point when it passes near that point.

The contribution of the ray is added to the total strength of the illumination at the observation point. This contribution is computed by considering the distance from the observation point to the ray and other ray parameters, such as the spread factor (which determines the variation of the amplitude of the ray because of the ray propagation and depends on the length of the ray path) and the number and nature of the reflections that the ray has suffered before approaching the observation point.

This procedure estimates (or extrapolates) the parameters of the ray that has the same ray path history (e.g., reflected/ transmitted on the same surfaces) and impacts the observation point. The estimation of the ray parameter is usually enough to obtain a good approximation of the contribution intensity of the ray to the total illumination at the observation point when the illumination is composed of incoherent waves.

The SBR strategy works well for many applications of visualization of scenes, wherein the ray effect order is not greater than two or three (and often the simple reflection is enough to describe the problem). Also, in these applications, the illumination is incoherent light, which simplifies the evaluation of the ray contribution because no phase computation of the field is needed.

The phase evaluation requires a very precise computation of the path length, which is difficult to obtain using the SBR strategy. In any case, the SBR needs to shoot an extremely dense beam of rays from the source point covering the entire spatial angle that illuminates the scene; typically more than 50,000 rays are shot.

The philosophy of the SIP strategy is different. Instead of shooting many rays from the source to find those that reach the observation point, the SIP attempts to solve the following inverse problems:

- Determine whether the direct ray connecting the source and observation points is occluded.
- Find all facets of the scene where reflected (or transmitted) rays can link the source and the observation points. After identifying these surfaces, the ray paths of the reflected (or transmitted) rays are obtained.
- Find all edges of the scene that can link the source and the observation point by diffraction. Determine the corresponding ray paths.
- Find all sets of facets that can join the source and the observation points by a second or higher order coupling mechanism and the corresponding ray paths.

The total strength of illumination is computed by adding the contribution of all ray paths found that link the source and the observation points. A rays path that connects the source and the observation points through reflections (or transmissions) can be computed in two different ways: using the image method for the case of a flat facets or by minimizing the total length of the path for curved facets.

The image method is based on image theory, which states that, given a source point and a flat facet, the reflected rays in the facet can be considered as rays radiated by the image source. The image source is a virtual source whose location is the specular image of the original source with respect to the plane that contains the flat facet.

Once obtained, and given the observation point and image position, the position of the reflection point for that observer can be obtained easily as the intersection of the segment that links the image with the observation point and the facet. These procedures can be generalized to obtain multiple reflections, simply by obtaining the nth-order image of the source, and from that, obtaining the complete trajectory of the multiple-reflected ray. Figure 6 illustrates this procedure.

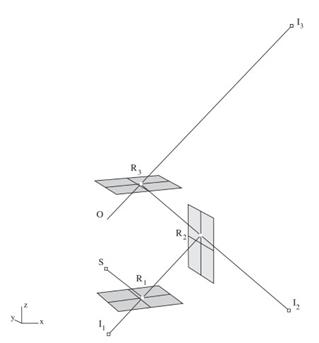
Figure 6. Example of the ray-tracing of a triple reflection using image method

If curved facets are used to model the scenario, then the image method cannot be applied. The trajectory of the ray is obtained using the generalized Fermat’s principle. This principle states that the length of the ray path that links two points is a minimum. A distance function can be defined whose value is the length of the ray as a function of the position of the points over the curved facet. The idea is to find the point whose distance function is a minimum, which determines this point as a reflection point.

This procedure has two disadvantages: First, the computational cost associated to the minimization process is high, and second, the possibility of local minima in the distance function can provide an erroneous solution for the position of the reflection point. Therefore, this procedure should be implemented with these points in mind, because no alternative can be used if curved facets are present in the scenario.

The SIP strategy is more complex and difficult to implement than the SBR because it solves inverse problems. However, the SIP is superior to the SBR for problems that require the illumination phase, diffractions, and high-order coupling.

These requirements occur in many applications of RTT for radio-wave propagation and other electromagnetic analyses, wherein the illumination has a coherent nature and therefore the phase plays a fundamental role. The SIP strategy permits a precise computation of all ray parameters for rays that arrive at the observation point. The application of the SBR strategy is easy but less accurate than the SIP strategy.