Formalizing and reasoning about the active behavior

Historically, the reactive behavior expressed as a set of condition ! action rules (IF condition holds, THEN execute action) was introduced in the Expert Systems literature [e.g., OPS5]. Basically, the inference engine of the system would ‘‘cycle’’ through the set of such rules and, whenever a left-hand side of a rule is encountered that matches the current status of the knowledge base (KB), the action of the right-hand side of that rule would be executed.

From the perspective of the ECA paradigm of ADBS, this system can be viewed as one extreme point: CA rules, without an explicit event. Clearly, some kind of implicit event, along with a corresponding formalism, is needed so that the ‘‘C’’-part (condition) can reflect properly and monitor/evaluate the desired behavior along the evolution of the database.

Observe that, in general, the very concept of an evolution of the database must be defined clearly for example, the state of the data in a given instance together with the activities log (e.g., an SQL query will not change the data; however, the administrator may need to know which user queried which dataset).

A particular approach to specify such conditions in database triggers, assuming that the ‘‘clock-tick’’ is the elementary implicit event, was presented by Sistla and Wolfson and is based on temporal logic as an underlying mechanism to evaluate and to detect the satisfiability of the condition.

As another extreme, one may consider the EA type of rules, with a missing condition part. In this case, the detection of events must be empowered with the evaluation of a particular set of facts in a given state of the database [i.e., the evaluation of the ‘‘C’’-part must be embedded within the detection of the events].

A noteworthy observation is that even outside the context of the ADBS, the event management has spurred a large amount of research. An example is the field known as event notification systems in which various users can, in a sense, ‘‘subscribe’’ for notifications that, in turn, are generated by entities that have a role of ‘‘publishers’’—all in distributed settings.

Researchers have proposed various algebras to specify a set of composite events, based on the operators that are applied to the basic/ primitive events. For example, the expression E — E1 E2 specifies that an instance of the event E should be detected in a state of the ADBS in which both E1 and E2 are present. On the other hand, E — E1;E2 specifies that an instance of the event E should be detected in a state in which the prior detection of E1 is followed by a detection of E2 (in that order).

Clearly, one also needs an underlying detection mechanism for the expressions, for example, Petri Nets or tree-like structures. Philosophically, the reason to incorporate both ‘‘E’’ and ‘‘C’’ parts of the ECA rules in ADBS is twofold: It is intuitive to state that certain conditions should not always be checked but only upon the detection of certain events and it is more cost-effective in actual implementations, as opposed to constant cycling through the set of rules.

Incorporating both events and conditions in the triggers has generated a plethora of different problems, such as the management of database state(s) during the execution of the triggers and the binding of the detected events with the state(s) of the ADBS for the purpose of condition evaluation.

The need for formal characterization of the active rules (triggers) was recognized by the research community in the early 1990s. One motivation was caused by the observation that in different prototype systems [e.g., Postgres vs. Starburst], triggers with very similar syntactic structure would yield different executional behavior. Along with this was the need to perform some type of reasoning about the evolution of an active database system and to predict (certain aspects of) their behavior.

As a simple example, given a set of triggers and a particular state of the DBMS, a database/application designer may wish to know whether a certain fact will hold in the database after a sequence of modifications (e.g., insertions, deletions, updates) have been performed. In the context of our example, one may be interested in the query “will the average salary of the employees in the ‘Shipping’ department exceed 55K in any valid state which results via salary updates.” A translation of the active database specification into a logic program was proposed as a foundation for this type of reasoning in Ref.

Two global properties that have been identified as desirable for any application of an ADBS are the termination and the confluence of a given set of triggers. The termination property ensures that for a given set of triggers in any initial state of the database and for any initial modification, the firing of the triggers cannot proceed indefinitely.

On the other hand, the confluence property ensures that for a given set of triggers, in any initial state of the database and for any initial modification, the final state of the database is the same, regardless of the order of executing the (enabled) triggers.

The main question is, given the specifications of a set of triggers, can one statically, (i.e., by applying some algorithmic techniques only to the triggers’ specification) determine whether the properties of termination and/or confluence hold?

To give a simple motivation, in many systems, the number of cascaded/recursive invocations of the triggers is bounded by a predefined constant to avoid infinite sequences of firing the triggers because of a particular event. Clearly, this behavior is undesirable, if the termination could have been achieved in a few more recursive executions of the triggers.

Although run-time termination analysis is a possible option, it is preferable to have static tools. In the earlier draft of the SQL3 standard, compile-time syntactic restrictions were placed on the triggers specifications to ensure termination/confluence. However, it was observed that these specifications may put excessive limitations on the expressive power on the triggers language, which is undesirable for many applications, and they were removed from the subsequent SQL99 draft.

For the most part, the techniques to analyze the termination and the confluence properties are based on labeled graph-based techniques, such as the triggering hyper graphs. For a simplified example, Fig. 1a illustrates a triggering graph in which the nodes denote the particular triggers, and the edge between two nodes indicates that the modifications generated by the action part of a given trigger node may generate the event that enables the trigger represented by the other node.

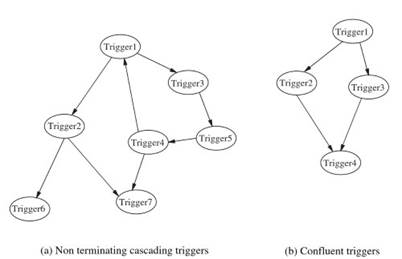
Figure 1. Triggering graphs for termination and confluence

If the graph contains a cycle, then it is possible for the set of triggers along that cycle to enable each other indefinitely through a cascaded sequence of invocations. In the example, the cycle is formed among Trigger1, Trigger3, Trigger4, and Trigger5. Hence, should Trigger1 ever become enabled because of the occurrence of its event, these four triggers could loop perpetually in a sequence of cascading firings.

On the other hand, figure 1b illustrates a simple example of a confluent behavior of a set of triggers. When Trigger1 executes its action, both Trigger2 and Trigger3 are enabled. However, regardless of which one is selected for an execution, Trigger4 will be the next one that is enabled. Algorithms for static analysis of the ECA rules are presented in Ref., which addresses their application to the triggers that conform to the SQL99 standard.