The electrochemical gradient
Consider a cell with an internal potassium ion concentration of 140 mM, immersed in an external solution with a potassium ion concentration of 4 mM (Table 3.2). There is a large difference in concentration, hence a large chemical gradient.
This would imply a high probability that a potassium ion can cross the membrane if we consider only the chemical gradient. However, due to the non-permeable negative charge present inside the membrane and the work of the Na/K ATPase, the asymmetrical ionic distribution is compensated for by the charges accumulated across the membrane.
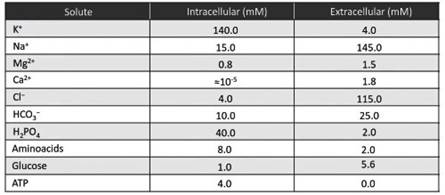
Table 3.2. Mean intracellular and extracellular concentrations of various solutes in a generic mammalian cell
The excess negative charge inside and the excess positive charge outside is balanced by the membrane capacitor, which is able to buffer the uncompensated charges and to restore the electro-neutrality of the solution (Figure 3.15). This creates a negative potential difference between inside and outside.
This behavior is precisely described by the Nernst equation, which is valid for all ions capable of crossing a plasma membrane in the presence of specific channels:
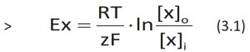
where x is a generic ion, Ex is the membrane potential related to ion x, R is the gas constant, which is 8.314472 Joules/(K.mole), T is the absolute temperature in Kelvin, z, dimensionless, is the valence of ion x, F is Faraday's constant, which is 96485.309 Coulombs/mole and represents the number of electric charges per mole of substance and [x]o and [x]i are the external and internal concentrations of ion I, respectively.
The RT/zF fraction of Equation 3.1, dimensionally expressed in Volts (tab. 3.2), takes into account the electrical gradient of the cell, while the dimensionless concentration ratio [x]o/[x]i takes into account the chemical gradient.
Equation 3.1 defines, for each ion freely permeable through a membrane and for a given ion concentration ratio between the inside and outside of the cell, the potential at which ion x has zero flux. For this reason, it is commonly defined as the equilibrium potential (for that particular ion) or even reversal potential, because positive or negative values of the membrane potential promote opposite movements of the ion x through the lipid bilayer.
In Equation 3.1, the relevant element is the equal sign: it associates the electrical potential E proper to ion x with its biophysical characteristics, defined by the ratio RT/zF and the ion concentrations inside and outside the cell, defined by the ratio [x]o/[x]i. The electrical equilibrium potential E for each permeable ion is therefore determined by the combined action of the electrical gradient and the chemical gradient, i.e., it is equal to the electrochemical gradient.
When, as a result of the flux of ion x, the membrane potential becomes equal to E (Equation 3.1), ion x has zero net flux because it is in electrochemical equilibrium with respect to the electric potential and the chemical potential.
Each ion capable of crossing the membrane through specific channels due to the presence of an electrochemical gradient has its own equilibrium potential, which is constant at constant concentrations and can be calculated using Equation 3.1 (tab 3.2).
Take, for example, the sodium ion. Its equilibrium potential, calculated according to Equation 3.1 with the concentrations given in Table 3.2, is +57.1 mV. If specific channels are present, sodium moves inwards with a membrane potential more negative than +57.1 mV (hyperpolarized).
On the contrary, sodium moves outwards if the membrane potential is more positive than +57.1 mV (depolarized). At a membrane potential equal to +57.1 mV, sodium ion net flux is null. The potassium ion, with an equilibrium, or reversal, potential of -89.6 mV (tab 3.2), has an outward flux for more depolarized membrane potentials, inward movement for more hyperpolarized membrane potentials and has zero net flux when the equilibrium potential and the membrane potential coincide.
The same behavior can be applied to all the permeable ions. The ratio [Ca]o/[Ca]i is very high and ECa very positive (tab 3.2). The chloride ion is an anion. z in the Nernst equation is negative and the ratio must be calculated with [Cl]i/[Cl]o.
By convention, the direction of the current takes into account positively charged ions. Inward charge movement is a negative current, and outward current is positive. Chloride ion movement out from the cell is like positive charge inward and thus the ion flux results in a depolarization of the membrane.
The role of chloride current, similarly to the potassium ion flux, has and inhibitory effect. If a chloride channel opens according with its equilibrium potential, negative charges enter in the cell with an hyperpolarizing effect.
Chloride has a negative equilibrium potential (tab 3.2), while the calcium ion, with a very positive equilibrium potential (tab 3.2), is only able to enter the cell in the physiological range of membrane potentials.
Date added: 2024-07-02; views: 407;
