Calculation Method . One-Dimensional Gas Dynamics

The goal of the calculation is to determine the characteristics of the pressure, temperature, mass, composition of the cylinder charge, and the characteristic curve of the mass change influenced by valves as a function of the characteristic of the crank angle during the charge cycle phase.

These quantities cannot be measured or can be measured only with great effort. Only the pressure can be indicated by means of a quartz sensor. The characteristic curves of these quantities are therefore calculated from a starting point by using numeric integration.

The initial values of the pressure, temperature, mass, and composition are determined at “outlet opens” by measuring or estimating, and their differential changes are calculated from this starting point using basic thermodynamic equations. On this basis, a suitable integration is applied step-by-step until all the values are known up to the time of “inlet closes.”

One-Dimensional Gas Dynamics. The filling and emptying method is a quasistationary singlezone model. In this instance, quasistationary means that transient processes are viewed as stationary for short intervals; i.e., the individual quantities (pressure, temperature) are dependent only on time but not location. Dynamic influences such as pressure pulses that, for example, arise in the ram tube charge and resonance charge cannot (of course) be included. Amplitudes and phase angles of the oscillations can support the charge cycle at certain rpm and hinder them and other speeds. The characteristic of the volumetric efficiency is essentially determined by means of the rpm and torque characteristic of the engine.

These oscillations are excited by pressure waves that arise when the valves are opened and closed and when piston motion occurs. The following figure illustrates the pressure curve determined with the aid of induced low pressure in the intake pipes of a slow one-cylinder four- stroke engine at 3000 rpm. At the beginning of the intake process, the downward movement of the piston generates a vacuum wave at the intake valve. This vacuum wave advances to the air filter that acts as an open pipe end. It is reflected as an overpressure wave, returns to the intake valve, and reaches it at IC (Fig. 10-52).

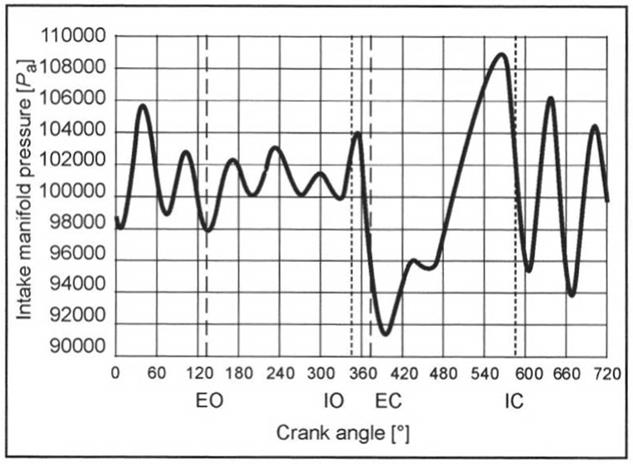
Fig. 10-52. Pressure characteristic in an induction pipe at 3000 rpm

In the one-dimensional simulation of the engine intake flow, the overall engine system is divided into individually abstract (i.e., simplified) elements such as the cylinder (Cl), air filter (PI 1), orifices (SB1, R1, SB2), and pipes (1-4) (Figs. 10-53 and 10-54).

Fig. 10-53. Schematic representation of an entire engine system

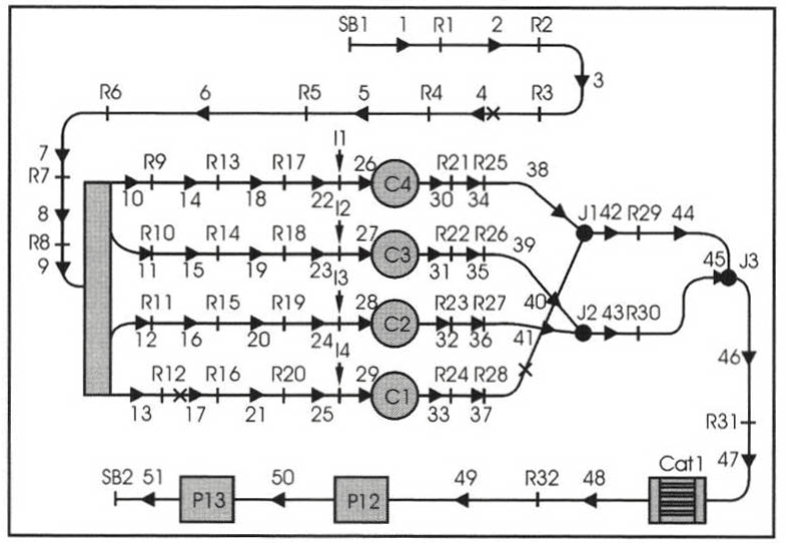
Fig. 10-54. Schematic representation of a four-cylinder spark-ignition engine

This is done assuming that the flow in the overall system can be described by a one-dimensional transient tubular flow in the pipe elements and by a one-dimensional quasistationary throttled flow in the components that connect the pipe elements.

The one-dimensional transient analysis within a pipe element assumes that the state quantities such as pressure p, density p, and speed и are sufficiently defined by averages in the individual pipe cross sections. Furthermore, it is assumed that there is no pulse loss because of internal friction in the flow. Only the friction of the flow against the pipe wall is covered.

This means that the processes in a pipe element such as the conversion of pressure energy into movement energy are irreversible only as a result of the included wall friction. A nonlinear inhomogeneous differential equation system is accordingly created for a one-dimensional transient tubular flow within the flow plane (x,t plane) based upon the conservation equations for mass, pulses, and energy:

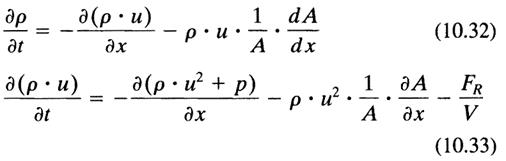
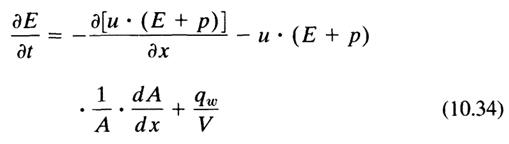
where F_R is the wall friction, V is the volume, q_w is the flow of heat, and E is the total energy.

To solve this problem regarding initial values and boundary values, we need information concerning the state at the pipe edges. This state vector is determined by the flow in the components that connect the pipe ends with each other. Stated simply, the filling and emptying method assumes that the flow is quasistationary through these throttling sites.