Calculating Charge Cycles

The simulation of the engine combustion process, especially combined with a one-dimensional simulation of the gas dynamics in the intake and exhaust systems, is today a generally accepted tool for predicting output data of engines in the design phase or during construction. It is also used for analyzing the charge cycle and the thermodynamic process of engines running on a test bench. Especially for the last application it can, when used correctly, offer information that could not otherwise be experimentally determined except at great expense.

Because of the complexity of the charge cycle process, an enormous amount of effort goes into its theoretical analysis. Depending on the respective question, a certain amount of simplification is required. For this reason, various calculations for special applications have been developed for analysis and simulation. A distinction is drawn among purely thermodynamic zero-dimensional models, one-dimensional models that couple zero-dimensional analysis with gas dynamics in the intake and exhaust systems, and three-dimensional spatial models (CFD).

Whereas a one-dimensional analysis makes it possible to describe the entire engine from the air filter to the exhaust system and thereby offers a temporal description and spatial (one-dimensional) description along the pipes of the processes, the three-dimensional CFD calculation is limited to spatial (three-dimensional) and temporal analysis of the processes in subsystems of the engine because of limited computer capacity.

The Filling and Emptying Method. The easiest way to describe the charge cycle in a real engine is the filling and emptying method. Since spatial gradients of the state variables are not covered by this method, the filling and emptying method belongs to the zero-dimensional methods of calculation. Despite this simplification, it is still sufficient in most cases for comparisons and an initial evaluation of the charge cycle.

In the filling and emptying method, the intake line and the exhaust line in the cylinder are viewed as containers whose contents are characterized by pressure, temperature, and material composition (Fig. 10-50).

Fig. 10-50. Model of the filling and emptying method

The filling and emptying method is based on the first law of thermodynamics:

To be able to determine the mass flows in the inlet and outlet, information must be obtained concerning the states at the inlet and outlet of the cylinder. Physically, strong three-dimensional flows occur through the valves that manifest jet disintegration and zones of turbulence. From a simplified perspective, the zero and one-dimensional models assume that the flow through these throttle sites is quasistationary. In this instance, “quasistationary” means that the state vector at the inlet and outlet areas of the throttle site (Fig. 10-51) does not change within a unit of time of the calculation, and that the change over time of the vector results from the sequence of different stationary states. Since the throttle site does not extend infinitely, this analysis is more applicable for smaller throttle sites in the direction of flow in comparison to the connected pipes (Fig. 10-51).

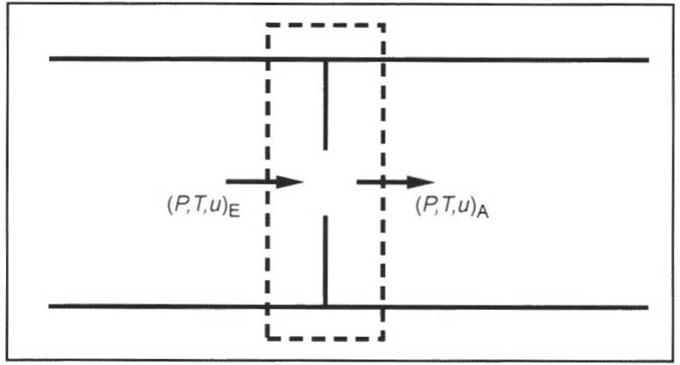
Fig, 10-51. State variables at a throttle site

Given these assumptions for this model, and the basic equations of the one-dimensional model, stationary flow can be used to calculate the state vectors (p, T, u)_E and (p, T, u)_A at the edges of the pipes. Using the continuity and energy equation for one-dimensional stationary flow, we obtain St. Venant’s theoretical flow equation that holds true when an isentropic, loss-free change in state in a flow cross section arises after the inlet and outlet surfaces of the quasistationary throttle sites. Since, however, the change in state is not isentropic and the pulse attenuates, this approach must be corrected. A stationary measurement is required that quantifies the thermodynamic effect of the flow phenomena that causes the pulse to attenuate.

This pulse attenuation manifests itself thermodynamically by an irreversible increase in the entropy of the fluid. The mass flow passing through the throttle site in an irreversible flow is smaller than the mass flow that would result with a loss-free flow. This loss is measured with the aid of the flow coefficient a that is defined as the ratio of the actual mass flow to the theoretical (isentropic) mass flow. The mass flows at the inlet and outlet are therefore calculated as follows:

coefficient a changes with the valve stroke and is experimentally determined using stationary flow experiments.