Calculating and Dimensioning Engine Bearings

A bearing is dimensioned in several steps during engine design work. The major dimensions, diameter and width, are determined primarily on the basis of the design parameters for the engine and mating components.

Once bearing loading has been calculated, it becomes possible, during the concept phase, to use specific bearing loading (F/b x d) as a rough reference value. Because of the great influence exerted by load characteristics, the ratio of width to diameter, bearing clearance, oil viscosity, and engineering details, exact calculations for bearing dimensioning have to be made as early as possible.

The primary results of calculation work are the selection of the appropriate type of bearing for the application and establishing the bearing dimensions, in conjunction with the acceptable boundary values.

Loading. The loading on engine bearings changes cyclically. The forces effective at the crankshaft are illustrated by a representative example in Fig. 7-255. These forces are made up of cylinder pressure and the reciprocating and rotating inertial forces.

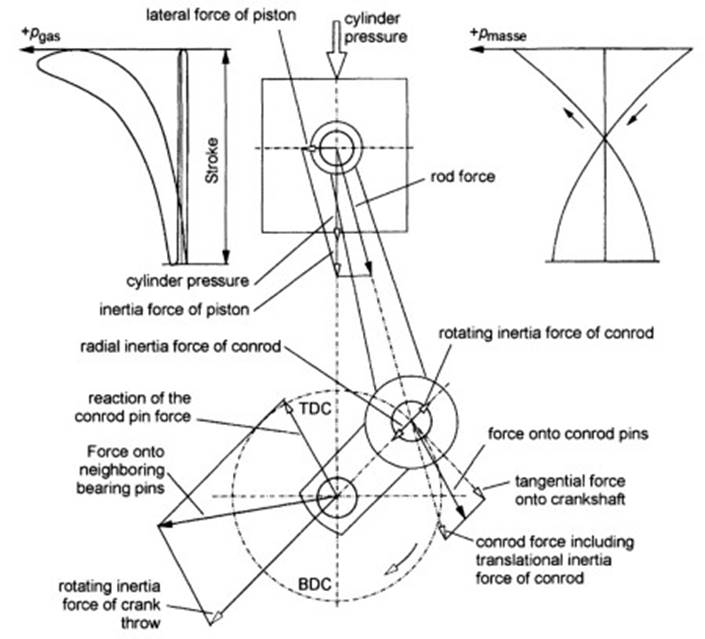
Fig. 7-255. Forces in the crank-shaft system

Figure 7-256 uses polar coordinates to show the progress of bearing forces—in both magnitude and vector— at the camshaft bearing in a diesel engine over a complete operating cycle and running at maximum torque. At higher speeds with lower loading, the peaks triggered by ignition decline and the ellipse representing inertial forces increases.

Fig. 7-256. Polar chart for forces at the conrod bearing in a diesel engine

When designing the crankshaft system, the bearing loads are normally calculated together with the stiffness and oscillation situation in the crankshaft, taking account of elastic deformations. Thus for the main bearings above all (statistically indeterminate bearing), one can ascertain more exactly the distribution of loading across the individual bearing points.

Having calculated cyclical loading in this way, one may then calculate the hydrodynamic pressures that are generated and the widths of lubrication gaps. The most commonly used method here is to calculate the bearing journal displacement path.

Bearing Journal Displacement Path. The displacement path that the journal executes in each full cycle, shown in Fig. 7-257, can be calculated with relatively simple means. The results are strongly influenced by the nature of the model (method after Holland-Lang or the mobility method after Booker), by the peripheral conditions for the pressure curve, and by the assumptions of oil viscosity.

Thus, it is possible to compare the results delivered by different programs only if these assumptions are identical. The acceptable boundary values, determined by applying experience from practical operations and drawing on test results for the calculated data, apply only for comparable calculation models.

The path is iterated across the full cycle through to convergence in steps of a few degrees of crankshaft angle. Calculations are carried out separately for each loading situation. As a rule, the values are ascertained for operation at nominal load and at maximum torque with low engine speed.

The most important results from the calculation are as follows:
- Smallest lubrication gap
- Maximum lubricating film pressure

Additional information is obtained, and this includes the oil throughput rate, hydrodynamic friction, and the resultant oil heating. The period through which the smallest lubrication gap remains in a certain area provides information on the concentration of friction energy and thus on the amount of wear to be expected.

The calculation of the displacement path is suitable particularly for parameter studies in an early stage of motor engineering, e.g., to determine the ideal layout for the balancer in view of the crankshaft bearings and/or the influence of design parameters such as the ratio of width to diameter or bearing play. Calculations for loading and the displacement path are often integrated.