What Filtration Is: On-Target Trajectories

One major challenge in predicting colloid transport in sediment is predicting the likelihood that colloids will reach grain surfaces. For a given colloid size, grain size, fluid velocity, and so on, the essential question is whether colloids lie on a fluid streamline that delivers them to a surface. This may seem strangely specific, but a useful analogy is to envision that you have fallen out of a raft into a raging, boulder-strewn river. Even if only at a subconscious level, you will avoid those streamlines that will smack you into a boulder.

In fluid dynamics terms, those streamlines are called forward flow stagnation zones (FFSZ). From the water quality perspective, the goal is to predict whether you, as a pathogen, will end up on the FFSZ of a boulder (or grain in porous media), thereby cleansing the downstream water. Your likelihood of intercepting a grain increases with your size, and it is enhanced if you swim in a panic in random directions across streamlines (e.g. colloid diffusion) or swim single mindedly across streamlines (e.g. colloid settling). Under groundwater flow rates and colloid densities similar to water (e.g. pathogens), the lowest interception rates (ⴄ) occur for the 1-2 µm colloid size range (bacteria sized) because of their lowest combined diffusion and settling.

The fraction of fluid flow field streamlines that are proximal to the FFSZ depends on the porosity of the porous medium and the flow rate. In this way, colloid filtration theory (CFT) boils down the complex tortuous flow field in porous media to an array of FFSZs, and this framework allows quantitative prediction of the transport distances that colloids may achieve before their concentration in water drops below some threshold that protects human health. CFT is a powerful framework from which to quantitatively predict colloid transport distances under conditions described below, with the caveat that nonspherical and/or size-distributed collectors or colloids produce complexities that are not accounted for in CFT.

Representative Collectors or Volumes. The first CFT model proposed by Yao et al. considered colloids approaching a single, isolated collector that was perfectly spherical and surrounded by an infinite fluid. This approach, as noted by Yao et al., produced velocity distributions that were likely poor representations of realistic porous media. The isolated-sphere approach was subsequently modified to employ a Happel sphere-in-cell geometry that included porosity, as well as a constricted tube geometry. The most popular, the Happel sphere-in-cell approach, considers the collector to be isolated from the influence of other collectors, perfectly spherical, and surrounded by an envelope of fluid. This approach was first employed by Rajagopalan and Tien and has been employed in more recent CFT models as it is conceptually straightforward and simple to upscale the results.

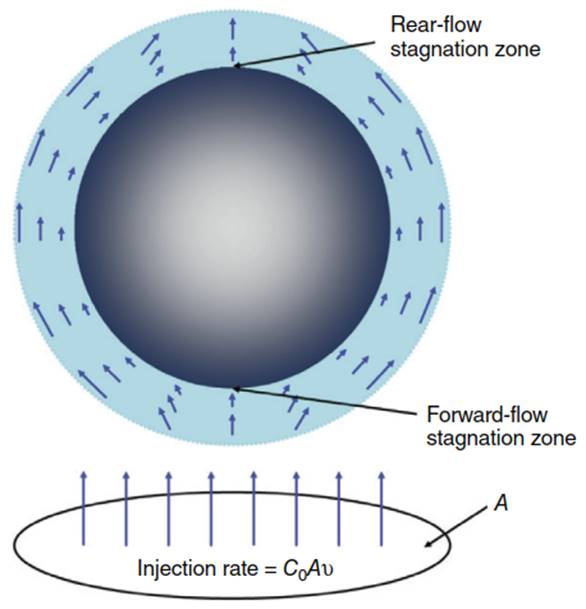
Figure 1. Illustration of a typical CFT model employing a Happel sphere-in-cell model. The geometry of the model is defined by the radius of the collector and the radius of the Happel cell (including the fluid shell). The blue arrows within the fluid shell represent approximate fluid vectors around the collector. The injection rate of colloids into the cell is calculated as shown using the concentration of approaching colloids, C₀, the projected area upstream of the cell, A, and the approaching fluid velocity, v

Figure 1, adapted from Ref., illustrates the Happel sphere-in-cell geometry along with the boundary conditions that would be employed by Eulerian mechanistic models. The flow field around the collector is assumed to be equivalent to Stokes (i.e. creeping) flow around a sphere and undisturbed by the presence of nearby collectors (approximate velocity vectors are illustrated in the figure). The fluid velocity (v) and colloid concentration (C₀) are considered uniform over the projected area upstream of the collector (A) (Figure 1).

Because an actual porous medium includes grain-to- grain contacts, it may yield flow phenomena inconsistent with Stokes flow around a Happel collector, including recirculation/vortice zones and low-flow zones. While Stokes flow incorporates low fluid velocities adjacent to the collector’s surface, the low/recirculating flow phenomena induced by grain-to-grain contacts likely extends this characteristic further outward. Thus, the flow field illustrated in Figure 1 and used in many mechanistic models is simplified relative to the expected actual flow field within a porous medium. To represent grain-to-grain contacts in a Happel-like model, Ma et al. developed a hemispheres-in-cell model with grain-to-grain contact with the line connecting grain centers oriented perpendicular to flow. Others developed simple or dense cubic packing cells as well as volumes of porous media, with the limitation that they have fixed porosities.