Nanoscale Heterogeneity as the Inferred Explanation

It has long been recognized that the calculated DLVO repulsion that prevents prediction of colloid attachment under unfavorable conditions results from the fact that a single value (ζ potential) is used to represent charge on each of the interacting surfaces, when, in fact, the surfaces may be heterogeneous at the nanoscale. Surface charge heterogeneities can arise from charge variability [67] and roughness on mineral surfaces (Figure 6).

Direct assay of surface heterogeneity (e.g. via X-ray photoelectron spectroscopy or other techniques) has no simple or direct translation to spatial variation in surface properties directly relevant to the colloid-surface interaction, e.g. ζ potentials. While the force volume approach of atomic force microscopy (AFM) directly yields colloid-surface interaction forces over an area, it is highly laborious to perform force volume imaging over a representative area of the collector at the resolution corresponding to colloid-collector interactions. Furthermore, colloidal probe measurements for <0.5 pm colloids are very challenging because of the small size of the colloid relative to the cantilever and the limited range of cantilever sensitivity (spring constant).

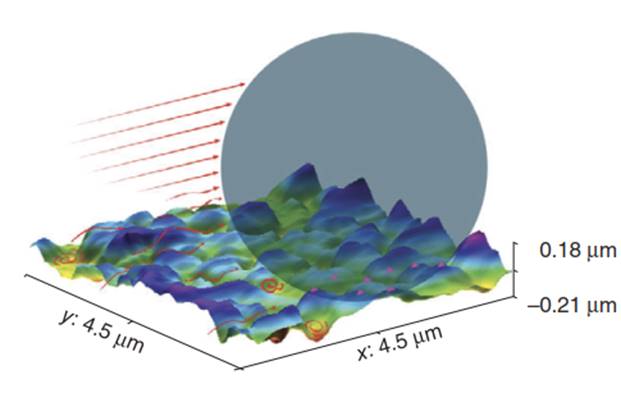
Figure 6. Schematic of nanoscale heterogeneity arising from roughness (surface topography) and charge heterogeneity (pink triangles). Arrows represent fluid velocity profile over rough surface

In addition to nanoscale charge heterogeneity, nanoscale roughness can locally reduce or eliminate repulsion. This is because the magnitude of repulsion between like-charged colloids and collectors scales directly with their radii of curvature. Within the space defined by smooth collector surfaces, roughness was recently shown to close the gap in attachment between favorable and unfavorable conditions for smooth surfaces from two directions. Under favorable conditions, roughness closed the gap from “above" by decreasing ⴄ relative to the upper bound (smooth theoretical surface), presumably via hydrodynamic effects. Under unfavorable conditions, roughness closed the gap from “below" by decreasing the magnitude of the repulsive energy barrier to attachment (decreased radius of curvature and increased adhesion via multiple points of contact, as well as possible increased charge heterogeneity via covariance with roughness.

Representative Nanoscale Heterogeneity in Simulations. To bypass the limitation that spectroscopic techniques cannot yet assay nanoscale heterogeneity in a way that is directly relevant to colloid-surface interaction, a representative nanoscale heterogeneity can be backed out from experimentally observed colloid attachment on silica and other minerals. In particle trajectory simulations based on mechanistic force and torque balance, heterodomains (nanoscale attractive zones) can be assumed to have a given size and surface coverage. These heterodomain properties are varied until the simulated colloid attachment matched experimental observations.

The essence of representative nanoscale heterogeneity is that it replaces the bulk surface characteristics with a representative heterodomain size and surface coverage that can explain colloid attachment under environmental conditions. The key element is that the zone over which van der Waals attraction and surface charge repulsion act is smaller than the colloid. These colloid-surface interactions decrease drastically with separation distance and so they become negligible beyond a short distance away from the point closest to the surface, because the colloid surface is curved.

The zone over which colloid-surface interactions are significant is called the zone of interaction (ZOI). Duffadar et al. determined that the radius of the ZOI (R_ZOI) increases with colloid size and increases with decreased solution IS. So, for a given heterodomain (nanoscale attractive zone) and colloid size, the net interaction can be attractive or repulsive, depending on how big the heterodomain is relative to the zone of interaction. Reduced solution IS increases the ZOI relative to the heterodomain and therefore may flip the interaction from net attractive to net repulsive (Figure 7).

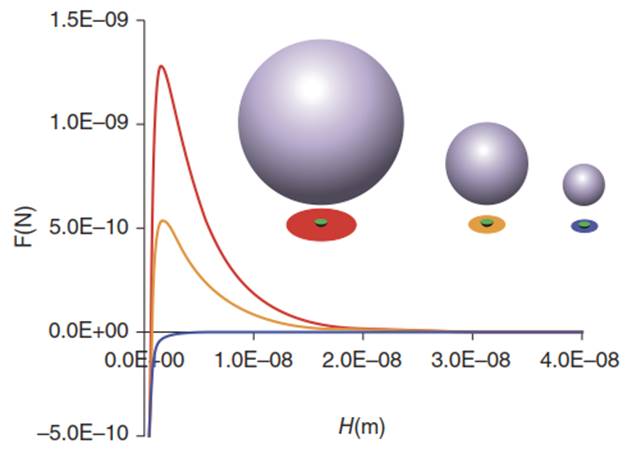
Figure 7. Colloidal force profiles as a function of colloid-collector separation distance (H) for 1.95,1.1, and 0.25 µm colloids, red, orange, and blue barriers, respectively. The projected outer circle represents the ZOI, and the inner circle represents an 80 nm radius heterodomain. The ZOI color and position corresponds to the force profile, with the left-most ZOI corresponding to highest barrier, right-most ZOI corresponding to absence of barrier, and intermediate ZOI corresponding to intermediate barrier. The repulsive force is greatest for the lowest ZOI coverage by heterodomains. Varied heterodomain size relative to ZOI would have the same effect, as would varied IS for a given colloid and heterodomain size (increased IS yields decreased R_ZOI).

For a given heterodomain size and IS, the net repulsive forcer (blue line = smallest, red line = largest repulsion) is directly related to colloid size, since the R_ZOI increases with colloid size (blue circle = smallest and red circle = largest colloid size), and the fractional coverage (of ZOI) by heterodomain decreases as colloid size (and R_ZOI) decreases relative to a given heterodomain size. Likewise, for a given colloid size and IS, the repulsive force is inversely related to heterodomain size, since larger heterodomains occupy greater fractions of the ZOI (red circle = smallest and blue circle = largest fractional coverage). Since the Debye length decreases with increasing IS, R_ZOI increases with increasing IS (for a given colloid size). Hence, for a given heterodomain and colloid size, repulsion decreases with increasing IS (blue line = highest IS and red line = lowest IS)

Successes of the discrete heterogeneity approach include prediction of colloid attachment under unfavorable conditions, as well as the experimentally observed detachment of colloids (i.e. a fractional release of the attached population) in response to perturbations in IS or fluid velocity. In addition to predicting experimentally observed colloid attachment and detachment under unfavorable conditions, the residence times of simulated colloids near the collector surface prior to attachment were found to predict the previously unexplained, experimentally observed non-log-linear distributions of colloids with distance from their source. The previously inferred “stickier" and “less sticky" subgroups were instead found to represent identical colloids having different outcomes, depending on how close they were to heterodomains upon intercepting the surface.