Thermal Insulation. Terminology and Mechanisms

Thermal insulation should minimise heat loss (or gain) allowing energy savings to be made, provide a comfortable environment for occupants, and protect a building from damage that might be caused by sharp temperature fluctuations (in particular, condensation). Heat exchange - by thermal convection, conduction, radiation and water vapour diffusion - cannot be prevented, but its rate can be reduced by efficient thermal insulation.

Terms used in calculating thermal insulation values. Although temperature is often given in degrees Celsius (°С), kelvin (K) is also used (OK = -273.15°C).

Quantity of heat is expressed in watt hours (Wh). (1 Wh = 3.6kJ.). Thermal capacity, the heat necessary to raise the temperature of 1 kg of material by 1 K, is a measure of the readiness to respond to internal heat or to changing external conditions. 1 kcal (= 1.16Wh) is the heat required to increase the temperature of 1 kg of water by 1 K.

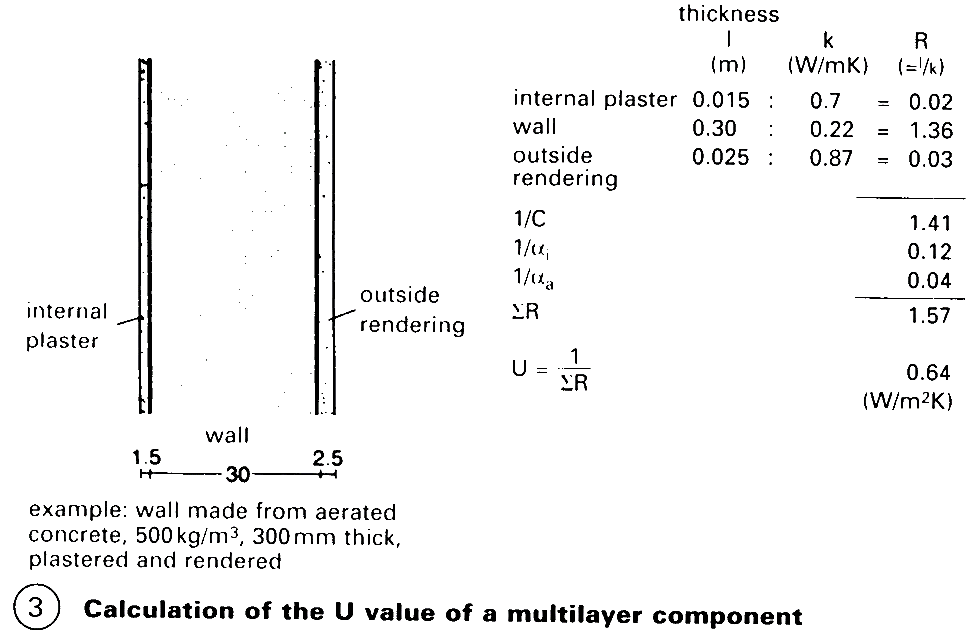
Thermal conductance (C-value), in W/m²K, measures the rate at which a given thickness of material allows heat conduction, based on temperature differences between hot and cold faces; no account is taken of surface resistance. Thermal conductivity (к-value or λ specific to a given material), in W/mK (or kcal/mhK), measures the rate at which homogenous material conducts heat: the smaller the value, the lower the thermal conductivity. Thermal resistance devalue = thickness/k), the reciprocal of thermal conductance (1/0, measures the resistance of material or structure with a particular thickness to heat transfer by conduction. Thermal resistivity (rvalue), is the reciprocal of conductivity (1/k).

UK thermal insulation standards have risen since 1990, under the new Building Regulations, in which the thermal insulation value is used to evaluate temperature variation in, and possibility of damage to, a structural component due to condensation.

The thermal boundary layer resistance, 1/a, is the thermal resistance of the air 'boundary' layer on a structural component: 1/a_a on the outside and 1/a; on the inside of the component. The lower the velocity of the air, the higher is the value of 1/a. Total resistance to heat flow ΣR is the sum of the resistances of a component against heat conductance:

The coefficient of thermal transmittance (U-value) - like thermal conductance - measures the rate at which material of a particular thickness allows heat conduction, i.e. the heat loss, and thus provides a basis for heating calculations, but the calculation is based on temperature difference between ambient temperatures on either side; account is taken of surface resistances of the structure. As the most important coefficient in calculating the level of thermal insulation, its value is specified in the Building Regulations, and is used by the heating systems manufacturer as a basis of measurement.

The mean U-value of window (w) and wall (W) is calculated as F being the surface area. Similarly, U_m, the coefficient of a building cell is calculated from the F and U values of the components making up the cell - window (w), wall (W), ceiling (c), floor surface (f) and roof area in contact with air (r) - taking account of minimum factors for roof and ground areas:

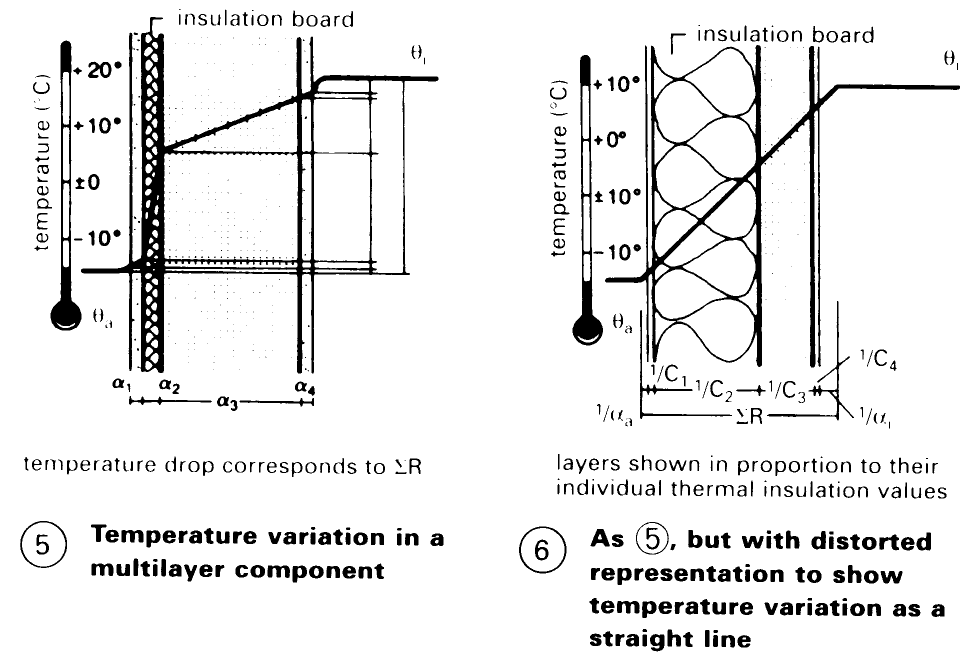
Heat transfer through a component: a quantity of heat is conducted through the internal air boundary layer and then the inner surface of the component; some of this heat overcomes the thermal insulation value of the component to reach the outer surface, overcomes the outer air boundary layer and reaches the outside air – (1). . Changes in temperature through the individual layers are in proportion to the percentage each contributes to the resistance to heat flow ΣR (3).

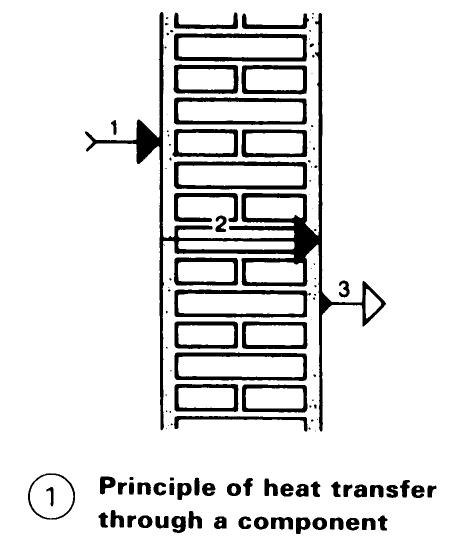
Example: If 1/a1 + 1/C + 1/a_a = 0.13 + 0.83 + 0.04 = 1.00, then 1/a1:1/C: 1 Aa_a = 13%:83%:4%. For a temperature difference of 40K between inside and outside, then: temperature difference across inner boundary layer = 13% of 40 К = 5.2 К; temperature across material = 83% of 40К = 33.2К; and temperature across outer boundary layer = 4% of 40К = 1.6К.

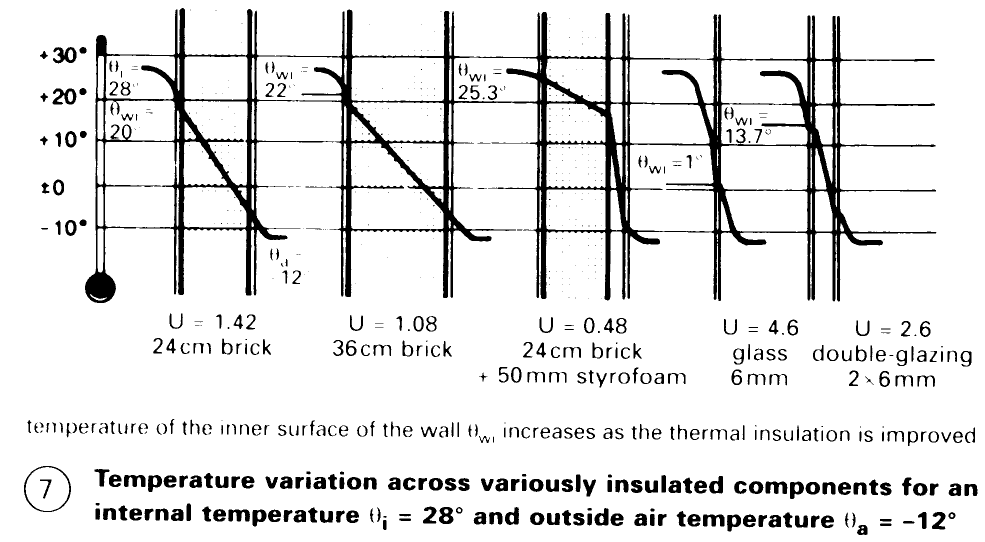
The lower the thermal insulation of the component, the lower is the temperature of the inner surface of the component - (7), and the easier it is for condensation to occur. Since the temperature varies linearly through each individual layer, this appears as a straight line if the component is represented to scale in proportion to the thermal insulation of the individual layers (5) - (6); the interrelationships are then more easily seen. The variation of temperature is particularly important in considering the expansion of the component due to heat, in addition to the question of condensation.

Thermal insulation should minimise heat loss (or gain) allowing energy savings to be made, provide a comfortable environment for occupants, and protect a building from damage that might be caused by sharp temperature fluctuations (in particular, condensation). Heat exchange - by thermal convection, conduction, radiation and water vapour diffusion - cannot be prevented, but its rate can be reduced by efficient thermal insulation.