Variable-orifice meters. Rotameter
So far the devices discussed have relied on a constriction in the flowstream causing a differential pressure varying with flow rate. Another category of differential-pressure device relies on maintaining a nominally constant differential pressure by allowing effective area to increase with flow. The principal devices to be considered are: rotameter, gate meter, and Gilflo.
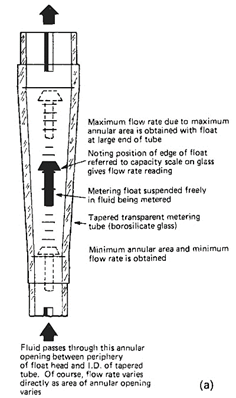
Rotameter. This is shown schematically in Figure 1.12 (a). In a tapered tube the upward stream of fluid supports the float where the force on its mass due to gravity is balanced against the flow force determined by the annular area between the float and the tube and the velocity of the stream. The float’s position in the tube is measured by a graduated scale and its position is taken as an indication of flow rate.
Many refinements are possible, including the use of magnetic coupling between the float and external devices to translate vertical movement into horizontal and develop either electrical transmission or alarm actuation. Tube materials can be either metal or glass depending on application. Figure 1.12 (b) shows an exploded view of a typical rotameter.
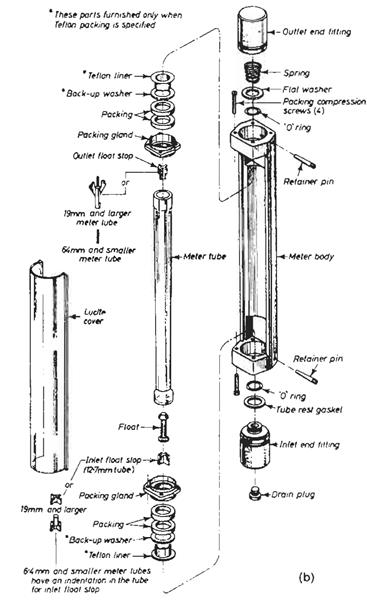
Figure 1.12. (a) Rotameter-principle of operation. Courtesy, ABB Instrument Group, (b) Rotameter-exploded view. Courtesy, ABB Instrument Group
Gate meter In this type of meter the area of the orifice may be varied by lowering a gate either manually or by an automatically controlled electric motor. The gate is moved so as to maintain a constant pressure drop across the orifice. The pressure drop is measured by pressure tappings located upstream and downstream of the gate as shown in Figure 1.13(a). The position of the gate is indicated by a scale. As the rate of flow through the orifice increases, the area of the orifice is increased. If all other factors in equation (1.21) except area A2 are kept constant the flow through the orifice will depend upon the product A2 * E or
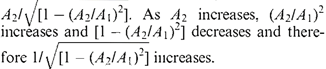
The relationship between A2 and flow is not linear. If the vertical movement of the gate is to be directly proportional to the rate of flow, the width of the opening A2 must decrease towards the top as shown in Figure 1.13 (a).
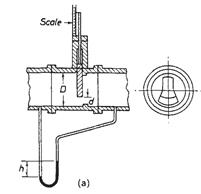
The flow through the meter can be made to depend directly upon the area of the orifice A? if instead of the normal static pressure being measured at the upstream tapping the impact pressure is measured. In order to do this the upstream tap is made in the form of a tube with its open end facing directly into the flow as shown in Figure 1.13 (b). It is in effect a pitot tube (see section on point-velocity measurement).
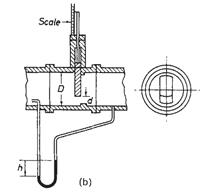
The differential pressure is given by equation (1.15), where h is the amount the pressure at the upstream tap is greater than that at the downstream tap:
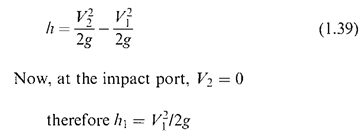
where h1 is the amount the impact pressure is greater than the normal upstream static pressure. Thus the difference between impact pressure and the pressure measured at the downstream tap will be h2 where:
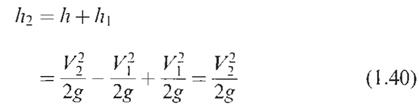
Therefore the velocity V2 through the section A2 is given by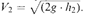 
The normal flow equations for the type of installation shown in Figure 1.13 (b) will be the same for other orifices but the velocity of approach factor is 1 and flow is directly proportional to Ai. The opening of the gate may therefore be made rectangular and the vertical movement will be directly proportional to flow.
The hinged gate meter is another version of this type of device. Here a weighted gate is placed in the flowstream, its deflection being proportional to flow. A mechanical linkage between the gate and a recorder head provides flow indication. It is primarily used for applications in water mains where the user is interested in step changes rather than absolute flow accuracy. The essential features of this device are shown in Figure 1.13 (c).
Date added: 2023-05-02; views: 338;