Empirical Example of Longitudinal Active-Life-Expectancy Calculations

As a first step in our example, the GoM measurement model was applied to 27 ADL, IADL, Nagi performance scores, and vision measures made in each of the six NLTCS for the period 1982 to 2004. That analysis showed that the 27 disability measures could be described by six types of disability profiles/dimensions found in commu­nity residents and a seventh discrete institutional resi­dence disability category.

With these seven disability scores, and the sample weights for individuals, it was possible to calculate a matrix of age-specific population disability transition parameters and age- and disability- dependent quadratic mortality functions estimated con­ditionally on the temporally current disability score values determined by the stochastic disability transition matrix. With disability dynamic equations and a disability- specific hazard function, life expectancy and ALE can be calculated conditionally upon the GoM disability scores by using generalizations ofthe well-known Fokker-Planck equations (Manton et al, 1993).

In addition, the disability scores can themselves be made functions of medical con­ditions and other possibly exogenous factors that may affect individual disability trajectories over age/time. For example, stroke may operate to decrement both the physical and cognitive functions of an individual.

This is one way to bring exogenous (control) variable information into calculations of endogenous changes of disability scores between NLTCS waves and to make projections of scores conditional on assumptions about trends in exogenous factors (i.e., either as observed or as may be generated by targeted interventions in control variables; Manton et al, 1993, 1994).

It was found (Table 1) that life expectancy estimates calculated using NLTCS data and exact times of death from linked Medicare files were quite close to those calculated by Social Security actuaries (SSA, Actuarial Study No. 116). This confirms that the NLTCS sample is representative of the survival experience of the entire U.S. elderly population, a property not always found in national health survey samples. This is illustrated in Table 1.

At age 65, the SSA cohort and NLTCS life expectancy values are quite close (i.e., 0.41 years higher in the NLTCS than for the SSA for males and 0.29 years lower than in SSA female cohort). The difference is, in part, due to comparing the cross-sectional experience in the NLTCS with the experience of the single year of age cohort born in 1917.

In addition, longitudinal life tables showing the time/ age dependence of both survival and disability changes may be calculated from the NLTCS. The disability dynamic dependent life table is presented for males and females in Table

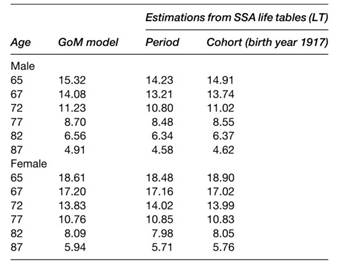
Table 1. Life expectancy for aged 65þ in 1982–2004 NLTCS

Table 2 was actually calculated as a complete (single year of age) table but, because of space considerations, we presented in the table only every fifth year of age up to 95 (where estimates begin to vary significantly due to small counts).

The columns to the right represent the propor­tion of life expectancy at that age that is expected to be lived in each of the seven disability states. The overall life expectancy is a continuously weighted mixture of life tables for each of the seven disability types. That is, there exists a separate life table for PT1 (persons with no functional impairment) for all persons exactly like that pure type; that is, g_i1 = 1. The life expectancy for this first type will be higher than the weighted average for the total, mixed population. Likewise, the life table for frail persons (i.e., g_i6 = 1) will have a much lower life expec­tancy than the total (mixed) population.

The first pure type (PT1) in Table 2 represents people with no chronic disability or physical limitations. The sec­ond and third types have partial limitations only in performing specific physical tasks. Pure type four is IADL- impaired; PT5 and PT6 represent persons with ADL dependency and with increasing levels of IADL impairment. The sixth type is frail; that is, highly ADL- and IADL- impaired. The seventh pure type represents respondents in institutional/nursing home residence. Such persons have significant functional limitations (e.g., 4.8 ADLs impaired on average) similar to the frail population; that is, PT6.

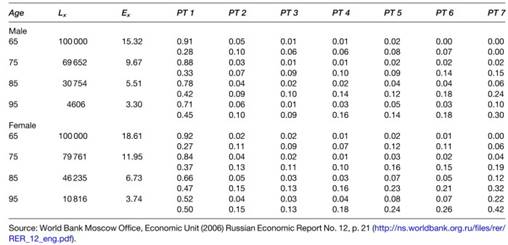
Table 2. Life tables with male and female cross-sectional disability covariates for 1982 to 2004 NLTCS

In Table 2, L_x and e_x have standard demographic interpretations; for example, that 30.8% of the male population with a mixed disability distribution survives from age 65 to 85, with life expectancy declining from 15.3 years at age 65 to 5.5 years at age 85. The first disability dimension represents persons free of disability.

The value in parentheses is the standard deviation of the disability score estimate. Since the space is convexly con­strained, the standard deviation of 0.28 for PT1 at age 65 suggests the distribution of nondisabled persons is concentrated in the interior of the K-dimension al disability state space. The mean value of 0.78 (standard deviation of 0.42) for the non disabled PT1 at age 85 indicates the burden of disability is much higher past age 85, with 16% of the male population living in the community in impaired states (i.e., 8% in highly impaired states 5 and 6) and 6% of males resident in nursing homes.

In the bottom panel of Table 2 is the corresponding abbreviated life table for females. Life expectancy is higher for females (18.6 years at age 65; 6.7 years at age 85) as is the age-specific prevalence of chronic disability at later ages; for example, 34% of females are impaired at age 85 compared to 22% of males.

Although the life tables are the end product of the ALE analysis done cross-sectionally (Sullivan, 1971), certain inter mediate transition parameter s are of interest if one wishes to examine the individual biological mechanisms, and their control parameter s, by which total and active life expectancy are generated over time in cohorts of indivi­duals.

One set of intermediate estimates are the parameters describing the change in the disability scores over time and the de pendency of those transition par a- meters on factors (e.g., disease or disability risk factors such as smoking, diabetes, or obesity) that are potentially controllable by specific interventions.

The second set of intermediate coefficients describes the risk of death spe­cific to disability state at a specific time and age. These two sets of coefficients interact over time to deter mine the life expectancy and risk factor distribution in the disability-dependent life tables previously described.

In Table 3, we present the matrix of disability-state transition coefficients calculated at ages 65 to 67 and ages 85 to 87. In the first row of the top panel (disability changes from age 65 to 67; or two-year transitions), 94% of the nondisabled male (and female) population (the first disability dimension or PT1) at age 65 remains nondis­abled at age 67.

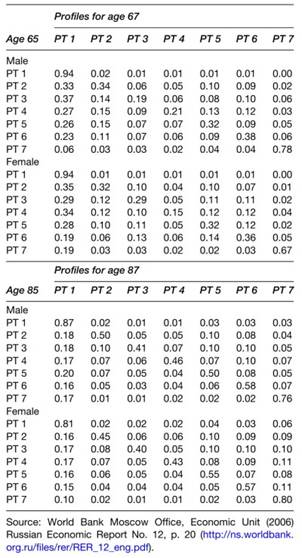
Table 3. Disability state two year transitions between profiles for age 65 and 85

The diagonal of the matrix represents the two-year persistence of persons in each of the seven disability states. For example, whereas males in the second pure type have little disability, though with some moder­ate physical performance limitations, after two years, only 34% of males remain in this type, while 33% of the type become nondisabled (i.e., move to PT1), and 26% become more severely disabled (with a transition to PT4 to PT7).

PT3 to PT6 have only modest persistence, though at ages 65 to 67 there is a significant likelihood of returning to a less disabled state. Only the group of severely disabled per sons resident in institutions has a high persistence and tends to remain in institutions.

At age 85 to 87, the disability changes for males (Table 3) show a persistence in disabled states that tends to be higher than at age 65 to 67 except for the nondisabled state (PT1). The return to the nondisabled state for females (column 1) is lower than at age 65, whereas the moderately disabled show a greater likeli­hood of their disability’s worsening.

The transitions for females show patterns similar to those of males, though with a higher retention in institutional residence. As a consequence, one way to view the transition matrix is as a web of transition paths between the two ‘anchor’ states of the convex disability space; i.e., PT1 for persons non-disabled an d PT7 for persons wholly disabled in institutions.

The intermediate states in the web connecting the two end points appear to be snapshots of the qualitative intermediate state changes that evolve at that age. A completely dynamic picture of changes would require attaching time parameters (waiting times) to the interme­diate states.

Interacting with these transitions is the risk of death for age-specific disability states. This is illustrated for both males and females in Table 4.

The hazard coefficients in Table 4 show that at age 65 there is a small survival advantage for females for most pure types and pure type interaction s (i.e., per sons whose disability status is described by a mixture of two, or more, disability dimensions).

That mean s, for a given disability profile, that female mortality at age 65 will be lower than for males. Those coefficients are, however, dependent on age, as shown in Table 5. Because the 0 (rate of aging parameter) for females is larger than for males, female mortality rates in specific disability states tend to increase more rap idly with age.

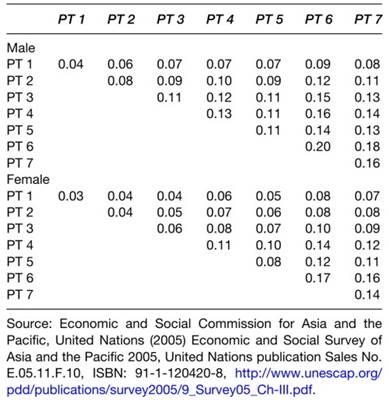
Table 4. Hazard matrix B at age 65 (proportion of deaths in one year) in NLTCS 1982-2004

In Table 5, we show the age-dependence of the male and female mortality functions, both without adjustments for the seven disability types and with adjustments for those disability types (scores).

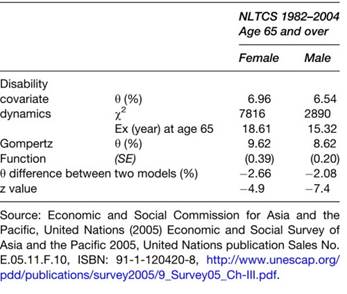
Table 5. The difference of senescence process (0) on disability covariatemodel and Gompertz model

The increase of mortality, specific to disability, is faster for females than for males (i.e., the 0 value is larger for females), indicating that a crossover will be expressed in male/female mortality trajectories at later ages. This is consistent with studies of gender differences in mortality and of disability trajectories.

Discussion. Active life expectancy is a useful measure of the amount of healthy, socially independent life expectancy existing in a particular national population. It has often been examined (e.g., Robine and Michel, 2004) by comparing, over time, cross-sectional life tables of the type proposed by Sullivan (1971) (see Manton et al, 2006b). It is now widely accepted as a basic measure of the quality of health in a country by WHO - especially in highly developed countries.

If, however, those measures are to be useful for study­ing how to intervene in the disablement/mortality pro­cesses determining active life expectancy, then longitudinal data on the functioning and survival of indi­viduals must be available, and those data must be analyzed longitudinally; that is, to explicitly identify the interac­tions of age-specific disability and mortality over time in well-defined groups (e.g., birth cohorts). This requires either special longitudinal health surveys or long-term population registries of health events and mortality.

We presented a stochastic fuzzy state model of these disability dynamics and their interaction with mortality that will allow more detailed study of the biological mechanisms that generate and sustain chronic disability of different types.

This will permit better estimation of the temporal parameters of disability processes - even at very advanced ages. Indeed, because longitudinal estimates of ALE require both age-specific estimates of disability dynamics and age and disability-specific mortality, addi­tional component parameters of the process are estimated that can be examined to help better understand sources of change in the processes.

With improved parameter estimates it will be possible to (1) better quantitatively forecast change in ALE and (2) better simulate the effects of specific interventions. Thus, although true longitudinal analysis of ALE pro­cess is more complex and has greater data require­ments, it is also intrinsically more informative and can be used to assess a broader range of issues, and in greater depth, than can the Sullivan-type cross-sectional estimates.

Furthermore, by using an explicit stochastic model of disability dynamics, more formal analysis of resource allocation models can be conducted. The formal analyses will better (more naturally and with fewer assumptions) describe population health and functional changes over time. This may lead ultimately to more effective and better-targeted strategies to improve ALE/LE ratios at late ages and thus to increase the human capital present at late ages in developed nations.