Excitable cells. The action potential
The model of the excitable cell that will be considered must have certain characteristics as described in previous chapters:
1. The shape of the cell is spherical to allow a homogeneous distribution of both the membrane potential and its variations. This is not always the case, since in an organism there are excitable cells with different shapes that certainly have transitory potential differences between one point and another in the cytoplasm.
2. The lipid composition of the membrane is homogeneous. There are many exceptions to this statement: for example, a membrane rich in cholesterol also influences the function of the ion channels by making the membrane in which the channels are embedded less fluid.
3. Ions respond to the laws of free diffusion as they move from one environment to another across the membranes using passive micro environments where the movement of ions and molecules may not follow the laws of free diffusion. Furthermore, passive ionic permeabilities do not always have the same diffusion coefficient as the one calculated in a solution because of the restrictions presented by the ion channel.
4. The cell must have at least two types of potassium channels, one type of sodium channel, a Na+/K+ ATPase, and a glucose transport system in its membrane and have potential energy in the form of a membrane potential.
The model cell under consideration has all of the minimal characteristics to be considered an excitable cell. It is able to generate and conduct functionally efficient potassium and sodium currents across the membrane using channels that have been suitably selected over the course of evolution with distinctive biophysical properties. The efficacy consists of the production of a far stronger response, from an energetic point of view, with respect to the stimulus received.
The action potential. The action potential is defined as the phenomenon of a transitory depolarization of the membrane potential from -65/-70 mV up to +35/+40 mV. The duration of an action potential varies from a few hundred microseconds, to a few milliseconds, up to several minutes, depending on the cell type. The membrane potential then returns, to the resting values within a time span typical of each excitable cell type (Figure 5.1).
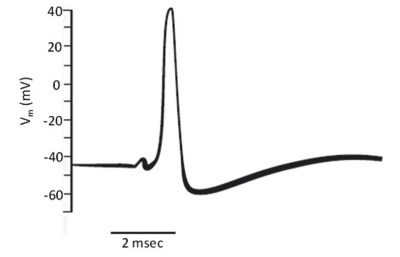
Figure 5.1. Recording of an action potential in a giant squid axon. Modified from Hodgkin and Huxley, 1945
From the beginning to the end of the voltage wave, the sum of the inward and outward currents must be zero to maintain electroneutrality of the solution. The energy required to perform this work comes from the potential energy stored across the membrane. The Na+/K+ ATPase, which works slowly and constantly to maintain a high level of potential energy in excitable cells, is not directly involved in the generation of the action potential.
The action potential is usually generated by an excitable cell once it is hit by a mechanical, chemical, electrical, light or thermal stimulus. A stimulus can be considered adequate if it is able to depolarize the cell membrane to the point of causing the all-or-none change in membrane potential. A stimulus is not necessary in cells where the action potential is produced spontaneously in a rhythmic pattern.
The cardiac pacemaker and intestinal peristaltic smooth muscle, for example, have automatic mechanisms which, by exploiting specific phenomena of membrane ionic conductance, are able to generate spontaneous action potentials that are rigidly regulated in frequency.
The resting membrane potential in a generic nerve cell is not stable over time (Figure 5.2), but can be correctly defined as dynamically stable. Membrane voltage oscillations are physiological events due to the actions of intrinsic cellular mechanisms and to external factors. The cell's response to compensate for spontaneous hyperpolarization or depolarization consists of the automatic activation of mechanisms which tend to bring the potential value back towards its resting value by means of positive or negative currents.
According to the convention of biological systems, negative currents are defined as those currents due to positive charges entering the cell or to negative charges leaving the cell through membrane channels, causing depolarization. Positive currents are defined as those currents generated by positive charges leaving the cell or by negative charges entering the cell through membrane channels, causing hyperpolarization.
The average membrane potential measured over a particular interval of time during which the number of charges generating a negative current are equal to the number of charges generating a positive current will be considered as the resting membrane potential. Therefore, if Im is the average membrane current, and Ie and Iu are the inward and outward currents, respectively, generated by the active and passive ionic fluxes present at the plasma membrane at equilibrium, the relationship is as follows:

The spherical excitable cell model under consideration is a very simple system from a dynamic point of view. It consists of an active component with ATP consumption, which creates and restores the electrochemical gradient exploited by passive components over time, mainly the conductances for sodium and potassium. At negative potentials such as the resting membrane potential, sodium has a large driving force, that is the difference between the membrane voltage and the equilibrium potential for a particular ion.
However, the sodium membrane permeability is close to zero, so no significant current is measured. On the contrary, potassium has low or null driving force because the resting membrane potential is close to potassium equilibrium potential, but a high membrane permeability. However, if the membrane potential moves away from its equilibrium and becomes more positive (Vm1 of Figure 5.3) or more negative (Vm2 of Figure 5.3), an outward or inward potassium ion flux generates a hyperpolarizing (outward) or a depolarizing (inward) current, respectively, to re-establish the equilibrium (Vm3 and Vm4 in Figure 5.3).
In both cases, the current responsible to maintain the resting membrane potential stable (IK1 or inward rectifying potassium current) is directly proportional to the voltage displacement. In the proximity of the cell average resting membrane potential, this potassium current allows outward-flowing or inward-flowing ions to maintain the resting membrane potential stable (Vm3 and Vm4 in Figure 5.3).
This is an important mechanism in excitable tissues which are activated only after they have been stimulated. The cardiac ventricular contraction is the clearest example. Systole occurs only following the command from the pacemaker cells. The IK1 potassium current is less important in nervous cells where the message is coded by the frequency of action potentials.
In the presence of the potassium current alone, which can quickly compensate for variations in the membrane potential, the cell is not able to generate a rapid depolarization. No matter how great the stimulus, the potassium current will always prevail. It is therefore necessary to activate a depolarizing current, which in the proposed model of the cell is carried out by sodium ions. The current must be voltage- and time-dependent.
The voltage dependency is evident since at -80 mV, the current is not appreciable, but a depolarization reaching -55 to -60 mV reaches the threshold for maximal activation of an action potential. At this potential, all the membrane currents follow Ohm's law and the result is activation at the precise moment of the voltage variation (Figure 5.4). If this occurs, it is clear that the net current though the membrane is null without a membrane potential variation.
Even if the hyperpolarizing current were greater than the depolarizing current, there would be an automatic adjustment of the latter and the establishment of a new membrane potential equilibrium between the inward (i.e., sodium) and the outward (i.e., potassium) current.
In order for the cell to generate a rapid depolarization, it is necessary that the membrane currents do not follow Ohm's law and that they have specific characteristics which take into account the voltage and time parameters which change at each instant.
In the following paragraphs, particular attention is devoted to the voltage dependence and time dependence of the membrane currents. The idea is to find a logical way in the model where, following a depolarizing stimulus, membrane currents retain the characteristics able to produce an action potential.
The model should show that in a generic excitable cell:
1. at the end of the membrane potential variation (action potential), the net current though the membrane is zero;
2. the stimulus causes a depolarization by inducing membrane capacitor current;
3. membrane ionic currents must be voltage- and time-dependent;
4. activation of ionic currents occurs upon membrane depolarization both for inward sodium and outward potassium ion flows;
5. activation of depolarizing sodium current allows the membrane potential to move towards the sodium equilibrium potential;
6. there are two types of potassium ionic permeability, one devoted to stabilizing the membrane potential and the second which becomes active during the excitation wave. The two currents have different voltage- and time-dependent characteristics. Both currents participate in the membrane repolarization process.
Date added: 2024-07-10; views: 355;
