Ionic membrane currents are voltage-dependent

In a current/voltage graph (I/V plot), the currents described by Ohm's law (equation 3.7) for potassium and sodium are linear (Figure 5.5) and the slope of the lines is the conductance or the reciprocal of the resistance, which is constant at each voltage value.

In the case of Figure 5.5, the conductance for potassium is greater than that for sodium. Such a system, if left uncontrolled, stabilizes the membrane potential at an intermediate value of about -20 mV, a value between the equilibrium potential for potassium (E_K) and that for sodium (E_Na).

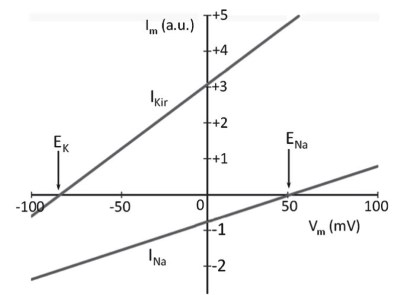
Figure 5.5. Linear trend of sodium currents (I_Na) and potassium currents (I_Kir), expressed in arbitrary units (a.u.), described by Equations 5.2 and 5.3.

In order to describe the sodium and potassium currents in the cell model under consideration, Ohm's law needs to be supplemented with the ion driving force, that is the difference between the membrane voltage and the equilibrium potential for a particular ion. Therefore, we must use the generalized Ohm's law, derived from Ohm's law (equation 3.8), applied to sodium

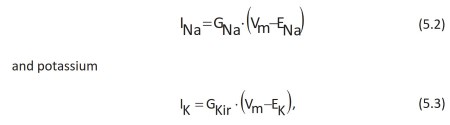
where V_m is the membrane potential and I_Na, E_Na, G_Na and I_Kir, E_K, G_Kir are current, equilibrium potential and conductance for sodium and potassium, respectively. In the cell model under consideration, E_Na is equal to +50 mV and E_K is equal to -90 mV (Data Sheet 3.2). For the membrane potential to stabilize at a potential close to the equilibrium potential of potassium, the sodium current must not be allowed to be active.

This phenomenon, shown in Figure 5.6 in the case of the sodium current, introduces a characteristic that belongs to all ionic currents in excitable cells: voltage dependence. To maintain the membrane potential at a negative value, the prevailing current must be the hyperpolarizing current of the potassium ion. At potentials between the equilibrium potential of potassium and –55 mV, the sodium current is practically absent.

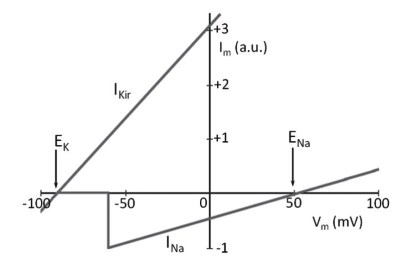
Figure 5.6. Linear trend of sodium (I_Na) and potassium (I_K) currents, expressed in arbitrary units (a.u.), described by Equations 5.2 and 5.3.

Thus, the membrane potential stabilizes at a value slightly more positive than EK. If a depolarizing stimulus from -70 mV to -55 mV is applied to the system described in Figure 5.6, the result will be instantaneous activation of the sodium current.

Under these conditions, the inward sodium current finds a hyperpolarizing potassium current already operating. Again, the membrane potential will stabilize at an intermediate value between the potassium equilibrium potential and the sodium equilibrium potential, at about -20 mV.

In order for the membrane to depolarize to positive potentials, the potassium current, which is decisive in maintaining the negative potential, must also be voltage-dependent. In practice, as shown in Figure 5.7, this particular current is active around E_K, but at a more depolarized potential following an appropriate stimulus, it reduces to a minimal flow.

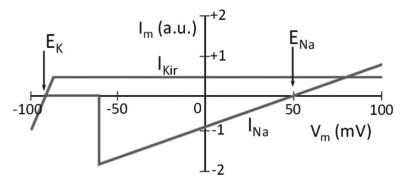
Figure 5.7. The potassium current is active at any membrane potential, but above a certain potential value it is constant and small

This behavior of the potassium current allows depolarization of the membrane to positive values, promoted by the entry of sodium ions, which shift the membrane potential towards the E_Na value. In this case, the membrane potential governed by the sodium equilibrium potential would be stabilized at a positive potential close to E_Na.

To return the membrane voltage to its resting state, it is necessary to activate a mechanism to repolarize the membrane. Essentially, the repolarization must be carried out by potassium current. This current has different kinetics from that described above, even if the overall characteristics are similar, such as the reversal potential and voltage dependency.

Its function must be to counteract the sodium current and therefore its activation must occur during depolarization, when the potential is greater than -55 mV. Its task is to repolarize the cell after a positive potential has been reached by the sodium current (Figure 5.8). Despite the activity and modulation of currents that we have assumed in the excitable cell model, voltage dependence is necessary, but alone is not sufficient to determine the action potential of the nerve cell.

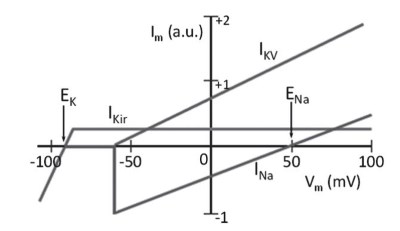
Figure 5.8. A voltage-dependent potassium current IKV is required to bring the potential back toward negative values

The second potassium current fails to conclude the depolarization/repolarization cycle and re-establish the negative potential after the transient change in membrane potential. Due solely to the voltage dependence of the currents (Figure 5.8), after an initial depolarization, the membrane potential would stabilize once again at an intermediate value between E_K and E_Na.

At potential values more positive than -55 mV, both sodium and potassium currents become active. Depolarization occurs because the sodium driving force is greater (V_m - E_Na) than the potassium driving force (V_m - E_K). However, the sodium current decreases as the membrane potential approaches E_Na. In parallel, the potassium current increases as the membrane potential moves away from E_K, and increases the driving force for the potassium ions to leave the cell. Again, at the end of the process, the membrane potential will stabilize at an intermediate value between E_Na and E_K, at about -20 mV.

In conclusion, we can say that the voltage dependence of the membrane currents is a necessary but not sufficient condition to guarantee the correct generation of the action potential in excitable cells. For correct development of the excitatory wave of the membrane potential, the membrane currents, in addition to being voltage-dependent, must be also time-dependent.