Interoperability Impact of Signal Waveform and Spectrum

It is often thought that signals with a different waveform and therefore different spectra are inherently less interoperable than those with identical waveforms and spectra. In particular, Figure 9.5 shows the spectrum of the GPS BPSK (1) C/A signal and of the Multiplexed Binary Offset Carrier (MBOC) spectrum of GPS L1C as well as Galileo E1 OS, BeiDou B1C, and QZSS L1C signals. The question, therefore, is whether the C/A signal is interoperable with the others.

The MBOC signal consists of two components, one being a BOC(1,1) waveform with 90.9% of the signal power and the other a BOC(6,1) waveform with 9.1% of the signal power. Most receivers will track only the BOC(1,1) component, either to minimize cost and/or bandwidth, or in the case of aviation, to minimize complexity. Therefore, we will examine the difference in tracking the C/A signal versus the BOC(1,1) component of MBOC.

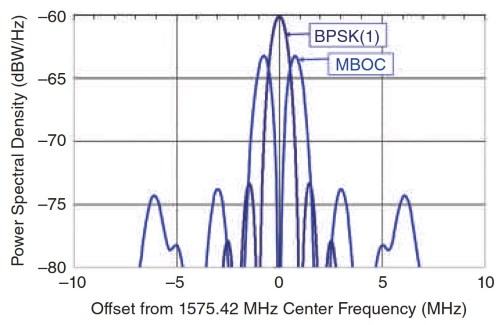
Figure 9.5. Spectra of C/A and of L1C

The most widely used method to track the spreading code of a GNSS signal is the early-minus-late (E-L) correlator. Variations of this also are widely used to reduce the effect of signal multipath, for example, the narrow correlator, the strobe correlator, the double delta correlator, or the multipath mitigation correlator. As explained in [16-18], subtracting a late correlator waveform from an early correlator waveform produces a waveform with three levels, +1, 0, or -1.

When the level is +1, a gate is open and the incoming (I channel) signal samples are summed. (The running sum also decays, and so older samples are replaced by newer samples.) When the level is -1, the gate is open but the signal samples are subtracted from the running sum. When the level is 0, the gate is closed and signal samples are ignored. (Ignoring signal samples when there is no transition to track improves the loop signal-to-noise ratio.)

Also, as explained in, the code tracking loop works to center the plus and minus gates on the spreading code transitions, the polarity of the gate being defined by the direction of the signal code transition. The result is that when the average of the running sum is not zero but is either positive or negative, that is the error signal which causes the code tracking loop to center the open gate times on the incoming signal code transitions. When the average of the running sum is zero, the code tracking loop is aligned with the peak of the code autocorrelation function.

The process for tracking code transitions of a BPSK(1) or a BOC(1,1) waveform is the same. The only significant difference is that a BOC(1,1) waveform has three times the code transitions per unit time than the BPSK(1), that is, about 500,000 per second for BPSK(1) and 1,500,000 for BOC(1,1). That improves the signal-to-noise ratio in the code tracking loop, but it does not cause one waveform to be less precise than the other except in extremely weak signal conditions.

If the receiver RF/IF bandwidth is wide enough, the transient response after a code transition should mostly settle before the next code transition. For the C/A spreading code, the minimum time interval before the next code transition is approximately 1 ps (977.5 ns). For BOC(1,1), the time interval is half that because the 1.023 MHz spreading code also is modulated by a 1.023 MHz square wave.

Therefore, the minimum RF/IF bandwidth for BOC(1,1) should be about twice that of the minimum C/A RF/IF bandwidth. Practically speaking, the bandwidth of a current narrowband C/A receiver may be adequate for BOC(1,1), and a receiver designed for BOC(1,1) certainly has sufficient bandwidth for the C/A signal. From a receiver bandwidth perspective, there is no adverse impact of processing both signals with the same hardware, especially because they have the same center frequency.

One characteristic which might seem to affect interoperability between BOC(1,1) and BPSK(1) is the autocorrelation function of each, as illustrated in Figure 9.6. When tracking BOC(1,1), it is important to avoid having the code loop lock to either of the “false” peaks at +0.5 and -0.5 spreading code chips from the main peak. Many papers have been written about how to avoid this trap. If both signals are transmitted from the same satellite, the BPSK(1) autocorrelation function, which has no such ambiguity, can be used to verify the proper alignment of the BOC (1,1) code tracker.

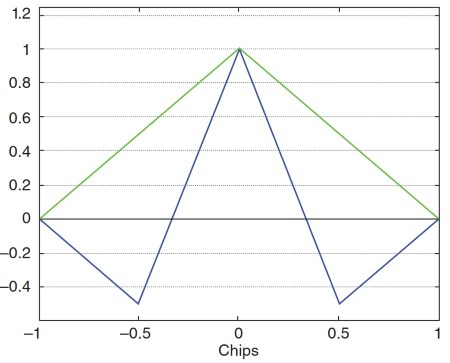
Figure 9.6. Autocorrelation function of BPSK(1) and BOC(1,1) signals

The relative “sharpness” of the two autocorrelation functions could imply that one yields better accuracy than the other. This has been a long-term fantasy. When GPS was first designed, it was assumed that the P-code would provide about 10 times the pseudorange measurement accuracy of the C/A code because the C/A autocorrelation function is 10 times wider than it is for the P-code. However, as is well known, some of the most precise measurements are made by C/A receivers. There are several reasons for this.

One is that receivers using a narrow correlator or a multipath mitigation correlator can use the same early- minus-late spacing (same gate width) for C/A as for P-code tracking. If both signals are filtered with the same RF/IF bandwidth, the rounding at the top of either autocorrelation function will be the same, which means that the accuracy of finding code transitions will be the same if the S/N in the code tracking loop is sufficiently positive. To improve the S/N, commercial, scientific, and aviation C/A receivers almost always employ a version of carrier-aided code smoothing, that is, the Hatch filter. This allows the code loop bandwidth to be reduced to 0.01 Hz or less. In most applications, the penalty of needing time for the filter to settle is of little consequence.

Therefore, it can be concluded that for most practical purposes the C/A BPSK(1) and the MBOC BOC(1,1) signals are fully interoperable in terms of code tracking accuracy.