Allometric Scaling in Biology: Size, Surface Area, and Metabolic Constraints Explained

Before going on to contrast specific organisms with respect to size, we consider briefly the role of shape and geometry as well as certain simple mathematical relationships in such comparisons. Geometrically similar bodies, i.e., those in which all corresponding linear dimensions are related in the same constant proportions, are said to be isometric (Schmidt-Nielsen 1984). This would be the case if two cubes of different sizes were compared, or two triangles that had corresponding angles equal and corresponding sides in a constant ratio. It is a mathematical inevitability (the Principle of Similitude noted earlier) that in isometric bodies area-related attributes increase with the square of linear dimensions, whereas volume-related features increase as the cube (Thompson 1961).

In large taxa, critical physiological processes and associated structures, such as those involved in musculature, respiration, and physical support, typically show adaptations (examples below) to partially offset such geometric realities, but these compensations are ultimately limited by size. This relationship also underpins the generality that larger taxa tend to be more specialized than smaller taxa.

A particular area:volume problem concerns efficient exchange of metabolites such as nutrients and various gases and waste products. Haldane (1956, p. 954) said that “comparative anatomy is largely the story of the struggle to increase surface in proportion to volume”. How is this achieved? The three evolutionary structural ‘solutions’ (Gould 1966) bearing wholly or in part on this problem have been: (i) a differential increase in surfaces among the more advanced animals (e.g., fish gills; lung alveoli; intestinal villi); (ii) a change in shape by flattening or attenuation without structural elaboration (e.g., the tapeworms); (iii) the incorporation of inactive organic matter within the soma (e.g., jelly in the case of Coelenterates; wood fibers in plants). To Gould’s list of solutions could be added the efficient partitioning of surface area:volume for the capture of resources—organisms as diverse as the fungi, sponges, plants, and corals all show essentially this same feature (Chap. 5).

Macro organisms are rarely isometric, though they may appear superficially similar in appearance. The term allometric or non-isometric scaling denotes the regular changes in certain proportions or traits as a function of changes in size (Chap. 2 in Schmidt-Nielsen 1984; see also West et al. 1997; Brown and West 2000). As most parents understand intuitively, when humans grow, their body proportions change—babies, for instance, have much larger heads relative to their size than do adults.

The general scaling relationship generally takes the form

Y = aW^b log Y = log a + b log W,

where Y is the biological variable of interest such as metabolic rate; W is a measure of body size such as mass; a is the normalization constant derived empirically and typical of the kind of organism; b is the scaling constant, also derived empirically. The equation in logarithmic form is a straight line with slope b and intercept log a.

The exponent b defines the general nature of the relationship as follows (Lindstedt and Swain 1988; Brown et al. 2000): When b is at or very near 1.0, Y varies as a fixed percent of body mass and would plot as a straight line with a slope of 1 on either linear or log axes. Indeed, such situations would be the sole instance where changes are strictly proportionate, i.e., isometric. Examples include mammalian heart size, and lung, gut, and blood volume, all of which increase closely in proportion to body size. If b is other than unity, the relationship is allometric and plots as a curve on linear axes. When b > 1.0, the increase in Y becomes relatively greater as size increases.

The skeleton in a shrew is about 4% of the animal’s body mass but accounts for 25% of the body mass of an elephant (Lindstedt and Swain 1988). How thick does the trunk of a tall tree (or a flagpole, for that matter) need to be to prevent it from buckling under its own weight or collapsing in an ice storm? The general mathematical result is that the diameter for taller trees should increase as the 3/2 power of the height, i.e., larger trees are disproportionately thick and this relationship holds throughout the life cycle (see later comments about the stems of small organisms).

When b is between 0 and 1, Y increases but only fractionally for each unit of increase in body mass. The famous 2/3 power law, S a V^0.67, was introduced earlier where we introduced the Law of Similitude. This can be visualized by comparing cubes of different sizes (Table 4.1 and Fig. 4.8). Many if not most biological scaling relationships are based actually on quarter powers of body mass (Delong et al. 2010). For instance, metabolic rate a M^3/4 may pertain to poikilothermic as well as homeothermic animals and, as originally proposed, to plants and microorganisms (West et al. 1997; Brown et al. 2000; however, see Reich et al. 2006; Price et al. 2012, and caveats below).

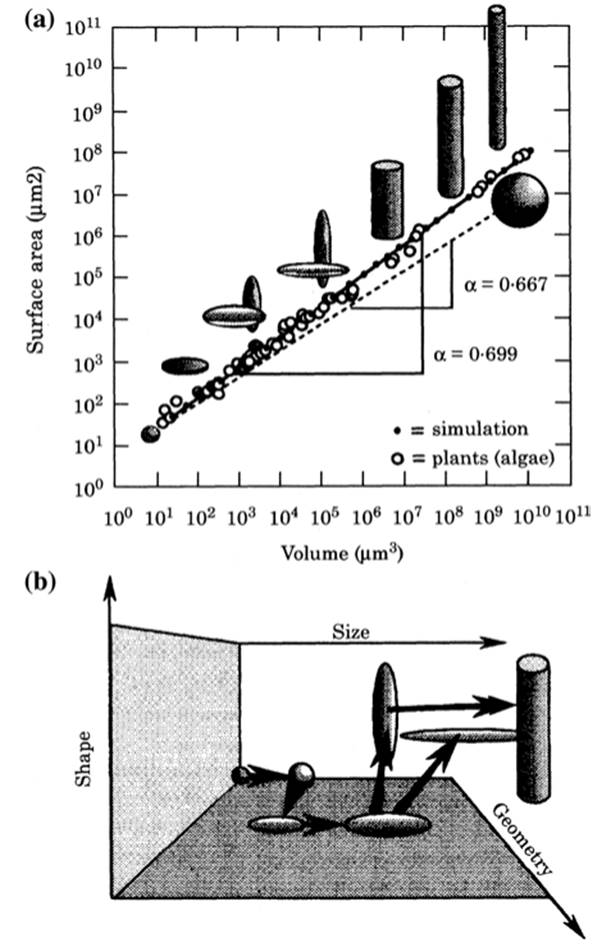
Fig. 4.8. Implications of the Law of Similitude. a Relationship between cell surface S and volume V for 57 species of unicellular algae (the straight line plot with slope 0.669). This is compared with a plot for spheres of different sizes (dashedline, slope 0.667) and with a computer-generated series of geometries (spherical to cylindrical) that maximize S to V as size increases. b Within this data set, the smallest unicells have spheroidal geometries and the largest are cylindrical. Within each category of geometry larger species tend to be spheroidal (flatter) than the smaller or more slender cylinders. From Niklas (2000); reproduced from Annals of Botany by permission of Karl Niklas and Oxford University Press, ©2000

Table 4.1. The law of similitude: the mathematics dictating declining surface area to volume for five cubes of increasing size

This means that for each 10-fold increase in size, metabolic rate increases, but by only 7.5-fold. In other words, weight-specific metabolism is higher in smaller animals. Indeed the approximate % power metabolic scaling relationship was once thought to be universal and became elevated to the status of a law, as ‘Kleiber’s Law, in honor of Max Kleiber who did seminal research on metabolic scaling in the 1930s and 1940s. Based on experiments with a broad survey of plants, however, Reich et al. (2006) conclude that whole-plant respiration scales about isometrically with total body mass (i.e., with a scaling component of 1, not %) and that the mechanisms underpinning scaling in plants are distinct from those in animals.

When b is negative, the slope is negative and accordingly the absolute value of Y is maximized in the smallest creatures. For various biological rates the exponent is close to -H. This means that while the heart of a shrew can exceed 1000 beats per minute, that of an elephant beats at only about 25-30 times per minute. The difference reflects the fact that resistance to blood flow is relatively higher in smaller mammals because they have relatively larger surface areas (supplied by capillaries where resistance is highest) for their size.

The argument of West et al. (1997), summarized above and subsequently extended (West et al. 2000; Brown et al. 2000), proposed a mechanistic general model for quarter-power scaling based on the common principle of transport of essential materials through branching fractal-like networks. Though extrapolated by the authors to organisms in general, the original model emphasized metazoans and subsequently was applied to plants (West et al. 1997; but see criticism and alternative by Price and Weitz 2012; Price et al. 2012). How well such a network model might apply to unicellular organisms, however, seems questionable a priori. Subsequent work by Brown and colleagues (DeLong et al. 2010; see also Huete-Ortega et al. 2012 for phytoplankton) revised the original postulate and showed that the slopes of log plots of active metabolic rate versus body mass were actually 1.96 (i.e., termed super-linear) for heterotrophic prokaryotes, 1.06 (i.e., linear) for protists, and 0.79 (sublinear; approximating % power function) for metazoans.

They hypothesized mechanisms to account for metabolic and body size scaling in each group: Rapid increase in rate as a function of size in the prokaryotes was attributed to an increase in the number of genes (thus more enzymes and biochemical networks and hence metabolic power); the approximate linear scaling in protists was arguably due to a linear increase with size in respiratory complexes in volume of mitochondria; sublinear scaling of metazoans reflected constraints imposed by differentiation of vascular and skeletal systems to supply increasingly large and complicated bodies. In overview, the consensus is that there is not yet and quite possibly never will be a universal meta- bolically based theory of ecology (Price et al. 2012).

In addition to the decreasing area-to-volume ratios as a consequence of increasing size, gravity constrains terrestrial bodies like flag poles and large organisms (Thompson 1961; Gould 1966). The oceans provide neutral buoyancy for whales. The giant sequoia tree has hard cell walls and massive arrays of supporting fibers and hence does not collapse under its own weight. Almost all animals have some sort of skeleton (hydrostatic, earthworms; exoskeleton, arthropods; endoskeleton, vertebrates). As alluded to earlier with respect to similitude (diameters increasing as the 3/2 power of height; or, equivalently, Height a Diameter^2/3), bones in animals and stems in plants must become disproportionately thick with increasing mass or height, if additional mass is to be accommodated (Chap. 5 in McMahon and Bonner 1983; Niklas and Spatz 2004).

The wings of birds are designed to provide lift and to be strong yet light in weight. Because weight varies as volume while strength of a device to support it varies as cross-sectional area, engineering considerations mean that to remain strong the arthropod exoskeleton must be thicker in larger animals. But beyond a certain point the shell would be cumbersome and would decrease survival. It is probably because of this structural constraint that insects were not able to evolve into forms able to occupy the niche now filled by passerine birds.

Microorganisms, in contrast, largely escape the scaling problems related to gravity, large size, and strength. Despite considerable variation in the size of fruiting bodies of the cellular slime molds, gravity has little effect on the relative diameter of their supporting stalks. Weight in this case has probably been negligible as an evolutionary consideration (Bonner 1982a), the stalks being geometrically similar, unlike the stalk of the relatively much larger mushroom or of a large tree discussed above, which become disproportionately thicker in the taller forms. Hence, Bonner and Horn (1982) have said that small organisms tend to have geometric similarity (isometry); large organisms have elastic similarity. The former organisms scale essentially as the function of one axis, that is, the diameter is directly proportional to the length (d a l) and a plot would have a slope of 1; the latter vary as two axes such that often but not invariably d a l^3/2 (McMahon 1973; McMahon and Bonner 1983; Niklas and Spatz 2004). How this 3/2 relationship arose during evolution of large organisms is explored elsewhere (Chap. 4 in Bonner 1988) and is one example of how selection for size in macroorganisms also affects shape (for general comments on engineering as it relates to organisms, see Wainwright et al. 1976).

By definition, a microorganism is small and its environment will obviously be small in absolute terms relative to that of a macroorganism. (Likewise, the impact of smaller organisms on their environment generally will be less than larger organisms.) This is clear for unicellular microbes such as bacteria and yeasts, as well as the unicellular protists and some small invertebrates such as the nematodes and rotifers. It is less straightforward for filamentous microbes, which technically are microscopic only by virtue of their narrow cross-section. If the component strands of the mycelial network of a fungus aggregate, however, the organism then becomes macroscopic, as happens when fruiting structures (mushrooms), mycelial sheets, or root-like rhizomorphs develop. Mushrooms form on a wet lawn in a matter of hours, moving the fungus through size and related changes in shape and gravity effects very quickly. So, size changes can occur abruptly. Nutrient signals appear to be the main trigger for the cellular slime mold to change from a disaggregated state of solitary, grazing amoebae to the social organism comprised of some 100,000 organized, aggregated cells (Kessin 2001).

Microbes are governed by the forces of diffusion, surface tension, viscosity, and Brownian movement (see Movement in a Fluid, below, and McMahon and Bonner 1983; Young 2006). Theirs is a world of molecular phenomena not noticed by macroorganisms any more than bacteria experience gravity. Even exclusively terrestrial microbes, including many protists and nematodes, are usually associated with liquid in some form. This may be mucilage or other secretions of their own making; soil capillary water; the interiors of plants and animals; or boundary layer films of various origins. Free water is required almost invariably for such activities as mobility, growth, and reproduction. Propagules are frequently released into or must escape through a liquid film. Surface tension can even be a major factor for the smaller macroorganisms. Haldane (1956) observed that whereas a human emerging from a bath carries only a thin film of water weighing approximately one pound, a wet mouse has to carry about its own weight of water and a wet fly is in very serious trouble.. /‘an insect going for a drink is in as great a danger as a man leaning out over a precipice in search of food” (p. 953).