Size and some metabolic implications. Movement in a Fluid

Peters (1983, see especially his Chap. 3) reviewed the literature and discussed at length the metabolic consequences associated with a particular size. Only a few of his many interesting points can be summarized here. A note on methodological differences should be made first. For higher animals, the power required to just maintain life is estimated from some minimum, so-called basal metabolic rate; this amount is supplemented by estimates of additional power required for each type of activity. For other taxa, such as the microbes, the term standard metabolic rate replaces basal rate, implying that the data are obtained under standard but not necessarily minimal conditions.

Peters has produced useful comparisons for unicellular organisms, poikilotherms, and homeotherms. The first of these is that the relationship between metabolism and body mass is similar for the three groups. Consider again the general equation, Y = aW^b. Because the value of a above is highest for homeotherms, declining in turn for poikilotherms, and then for unicells, metabolic rate for a hypothetical 1-kg organism in each group declines comparably. As Peters remarked, one ecological implication is that the relative demands of the three types of organisms on their bodies and on the environment must decline in similar fashion.

Consequently, homeotherms need high resource levels and have to be relatively efficient in resource utilization. Heat loss or heat gain is a size-related consideration for homeothermic macroorganisms. A human, for example, consumes about 1/50 of its weight per day, a mouse 1/2 its weight. The design of a warm-blooded animal much smaller than a mouse becomes impossible because the organism could not maintain a constant body temperature (Chap. 2 in Thompson 1961). Peters (1983, p. 33) calculated that small mammals degrade about 10 times as much chemical energy per unit time as would an equivalent mass of large mammals. In contrast, the constraint at the upper extreme pertains to heat dissipation because the larger the animal the greater its heat production relative to heat loss.

This is manifested by lethargy and various heat exchange devices or behaviors of various kinds to promote cooling. Heat production for the mouse and heat dissipation for the elephant is both a consequence of the fact that heat generating capacity varies as the cube of the linear dimension while loss depends on surface area, which varies as the square.

If power production is expressed instead in specific terms (watts kg^-1), the rate of energy consumption decreases with body size. This means that within each of the three groups the maintenance cost for large organisms is less than that for the same amount of smaller organisms. Another way to look at the same issue is to ask what the maximum amount of biomass is that could be supported per unit of energy supply (kg watt^-1). Thus, it turns out that the same amount of energy could support about 30 times more poikilotherms (and still more unicells) than homeotherms. Within each class, a greater biomass of the larger than the smaller organisms could be sustained per unit of energy flow.

Crude estimates can be made of turnover time, i.e., the time needed to metabolize an amount of energy equivalent to the energetic content of tissues (Peters 1983, pp. 33-37). Again, among organisms hypothetically of equivalent weight, turnover times are shortest for homeotherms, and progressively longer for poikilotherms and unicells in which energy is mobilized more slowly. Within each metabolic group, energetic reserves of the larger organisms last longer than those of the smaller.

Movement in a Fluid.Planktonic microorganisms such as bacteria, diatoms, dinoflagellates, and many of the green algae live in a world dominated by fluid mechanics. Likewise, intestinal and soil- or sediment-inhabiting bacteria live in viscous environments quite unlike those typically inhabited by macroorganisms. One criterion of life in such habitats is the Reynolds number (Re), a dimensionless or relative velocity related to movement in a fluid that expresses the ratio of inertial forces (i.e., forces required to accelerate masses; numerator) to viscous forces (forces required to cause shear; denominator) as follows:

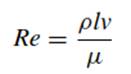
Where
Re Reynolds number
p fluid density, g/cm
l characteristic organism length, cm
v characteristic organism speed, cm/s
µ fluid viscosity, g/cm s

McMahon and Bonner (1983, see their Chaps. 5, 6; Berg 2004; Stocker and Seymour 2012) discuss some interesting implications of Reynolds numbers, particularly as they apply to the propulsion of microorganisms. For the movement of small organisms (i.e., with short lengths and speed), viscous forces (density and frictional components) dominate, and the Re is low. Conversely, for large organisms, inertial forces dominate and Re is high. The blue whale, because of its huge size and relatively fast speed, swims at a Re of about 10⁸, the porpoise of 10⁵, while that for a moving bacterium is comparatively miniscule at about 10^-6. To small organisms water appears very viscous, perhaps analogous to how quicksand would appear to humans; motility is further constrained where increased viscosity, surface effects, or porosity impair swimming (Fenchel 2008). Interestingly, some microorganisms (e.g., some ciliates, copepods) have mechanisms to momentarily escape a low-Reynolds number world by jumping to enhance nutrient uptake or to attack prey. Guasto et al. (2012) discuss these adaptations and the many ramifications of life in fluid environments.

For planktonic microorganisms, morphology and flagellar propulsion systems appear to be optimized for efficient movement. Inertial forces of water, used to advantage by fish for movement, are of little consequence at a low Re. A microscopic whale would get nowhere by its mode of propulsion. Conversely, a bacterium or protozoan could not swim like a whale. Their motion is dominated by the viscosity component which also means that, unlike fish, they have essentially no glide distance once their propulsive engines have stopped. It does not coast. Furthermore, at a low Re, swimming is completely reversible. In theory, if a microorganism moved ahead and then back by exactly the same number of propulsive movements, not only would it return to the identical spot but all the displaced water molecules would also return to their original places.

Finally and most fascinating of all are the implications for the design of the propulsive equipment. The problem, because of the reversibility of movement at low Re, is that if microbes had to move by solid ‘oars’ they would go nowhere (forward on the thrust, followed by an equal distance back on the return stroke). The novel solution is provided by the form of the propulsive equipment: flagella in bacteria, which are anchored at their base and rotate like propellers, and flexible oars in the form of related but structurally distinct cilia for larger microorganisms such as the protozoa (Son et al. 2015). The cilium is held straight out on the power stroke but collapses parallel to the body for the return, which reduces drag. (It is noteworthy as an aside that although ciliated organisms range in size over two orders of magnitude, in general, cilia length and frequency of beating remain approximately constant. This means that most swim at about the same speed of about 1 mm/s or approximately 10-fold that of a flagellated bacterium.)

To summarize, physical constraints imposed on an organism vary with its size. The elephant with a huge bulk supported by a massive skeletal system experiences a world dominated by gravity, area:volume scaling, and thermodynamics. The tiny mycoplasma, without even a cell wall for support, knows nothing about gravity or the complexities of multicellular homeostasis, and exists partially suspended in a world governed by fluid dynamics and diffusion phenomena. Such physical determinants are probably as important in evolution as they are in civil engineering (Lindstedt and Swain 1988). These constraints influence shape— shapes possible for one organism are not options for another—means of locomotion, speed, and many other related features that are discussed further below. There is probably an optimal size associated with each type of activity (Haldane 1956; Pirie 1973).