Exciter Forces and Exciter Work

The vibration-exciting torsional force (tangential force) is composed of
- Gas torsional force (Fig. 6-59)
- Torsional force of the oscillating inertial forces (the rotating inertial forces do not participate in the excitation) (Fig. 6-60)

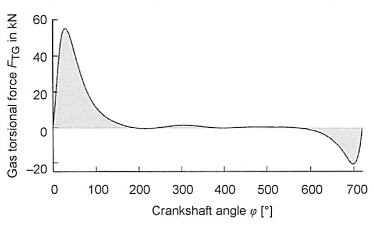
Fig. 6-59. Gas torsional force characteristic of a fourstroke diesel engine

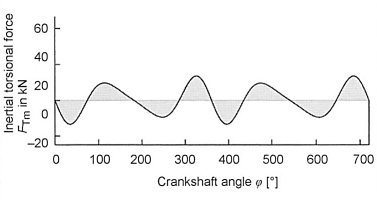
Fig. 6-60. Inertial torsional force characteristic of a fourstroke diesel engine

Since the gas torsional force is a function of the load (specific work), and the inertial torsional force is a function of the square of the rpm, their influence is investigated separately.

The gas torsional force cannot be described by a closed function and is therefore subject to a Fourier analysis; this is composed of a static component (nominal load torque) and a dynamic component (a basic vibration and overlapping harmonics). The exciting frequencies are, hence, the basic frequency (number of work cycles per unit time) and their integral multiples. They are proportional to the crankshaft speed. All of these exciting frequencies can resonate with one of the natural frequencies (Fig. 6-61).

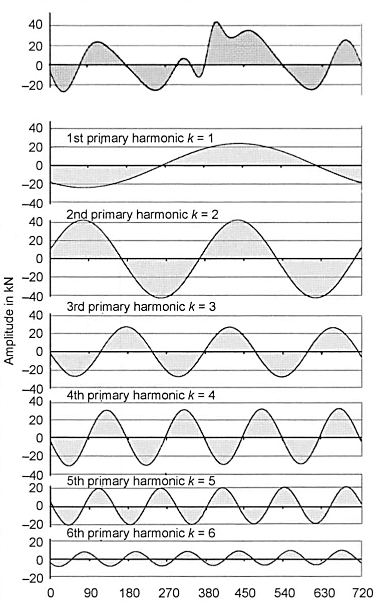
Fig. 6-61. Fourier analysis of a tangential force diagram: The tangential force curve is composed of the first six harmonics

The exciter work is the essential determinant in exciting vibration. An exciter force (resulting exciter force amplitude from the amplitudes of the gas and inertial torsional forces for the individual exciter frequencies) generates a greater excursion the farther it acts from the oscillating nodes (exciter work = exciter force × vibration amplitude). The phase angle of the exciter forces, i.e., their sequence over time, is represented in phase direction diagrams. The phase direction diagrams of the individual orders result from the order throw diagram of the 0.5 order (four-stroke) and of the first order (two-stroke) (Fig. 6-62).

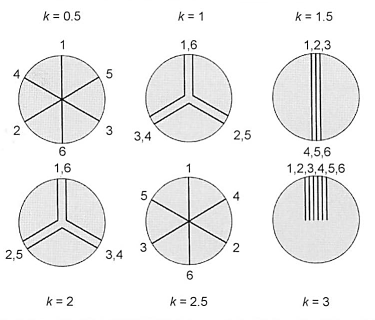
Fig. 6-62. Phase direction diagrams up to the 6th order for an inline six-cylinder four-stroke-crank gear

Taking into consideration the vibration amplitude of the individual throws and the phase shift (firing sequence), we get the effective exciter force of the engine.

The relative crankshaft excursions of the individual cylinders are added geometrically in the direction of the rays of the phase direction diagrams. This shows us that certain orders are particularly dangerous because their geometric sum becomes very large. The geometric sum is described as the specific exciter work, i.e., exciter work of the engine in reference to force 1. Depending on the order and phase angle, the specific exciter work assumes different values.

The amplitude—the absolute excursion—of mass 1 is calculated from the equilibrium of the excitation work and damping work (per vibration). This allows us to determine the absolute excursions A of the individual masses of the substitute system:

The relative twist Δφ of the masses x and x + 1 from the rotational oscillation stresses the crankshaft in addition to static torsional force.

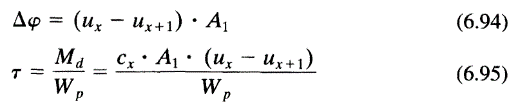
In particular, the gas forces excite vibrations of an order that are an integral multiple of the number i of ignitions within a crankshaft rotation.

- Four-stroke engine: i = z/2 ignitions per crankshaft rotation
- Two-stroke engine: i = z ignitions per crankshaft rotation

All integral multiples of z/2 (four-stroke) or z (two-stroke engine) are dangerous since the exciters of all the cylinders are aligned for these orders. The critical speeds result from the intersections of the main harmonics with the exciter frequencies. The extent of the danger to the engine at the individual critical speeds can be found by calculating the resonance excursions of the crankshaft.