Rotational Oscillations. Fundamentals

The crank gear is a spring-mass system that is excited to vibrate (oscillating rotational movement of the sequential individual masses on the shaft) by the periodic torsional forces (tangential forces) that overlap the actual rotational movement of the crankshaft. The rotational movement of the crankshaft therefore comprises three components:

- Even rotation corresponding to the speed
- Speed fluctuation as a result of the uneven torsional force characteristic (tangential force characteristic) over a power cycle ("static speed fluctuation")
- Vibration over the displacement angle caused by the torsional force ("dynamic speed fluctuation")

The movement of the system is described by the angle of twist of the moments of inertia in comparison to the initial position.

The kinetic energy stored in the moments of inertia is released to the coil springs and converted into potential energy in order to be reconverted back into kinetic energy. Given loss-free energy conversion, the free vibrations would last forever; the natural frequency depends exclusively on the system properties of spring rigidity and mass. Because of the resistance to the movement, energy is withdrawn from the system and converted into heat: The vibration is suppressed and slows at a greater or lesser rate depending on the damping.

If a periodic force acts on the system from the outside, then it forces the system to assume different vibration behavior; the system vibrates—after a transient phase— at the frequency of the exciting force. If the natural and exciting forces correspond, resonance occurs. Without damping, the vibration amplitude would assume an infinite value. However, the always-present damping limits the amplitude, and the size of the amplitude depends on the strength of the damping. This situation is illustrated by the magnification function V as a function of frequency ratio Ω/ω. [The magnification function is the ratio of the (maximum) vibration amplitude of the system to the amplitude that would result if the spring of the system were under a static load from the exciting force.]

If the path of the vibration amplitudes of the individual masses is represented over the length of the shaft as a curve trace, we get the mode of vibrations with the zero transition points of this curve as vibration nodes in which two neighboring masses vibrate in the opposite direction.

No rotational oscillation movement occurs at these points (certainly rotational oscillation stress, however) (Fig. 6-53).

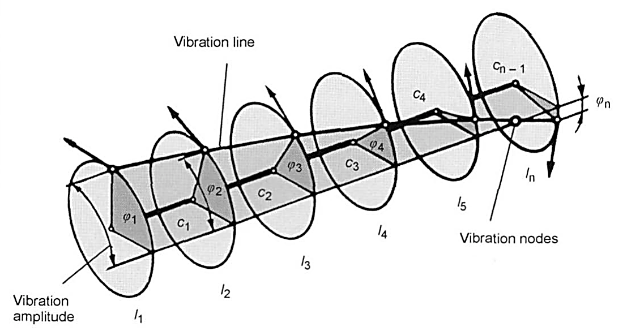
Fig. 6-53. Diagram of a rotational oscillation system

For each possible form of vibration, there is a natural frequency that the system can use to execute free vibrations in the relevant mode of vibration. The mode of vibrations and the natural frequencies depend on the size and distribution of the torsional rigidities and the moments of inertia in the system.

Since the resonance can lead to vibration amplitudes that can destroy the crankshaft (Fig. 6-54), it is important to identify such dangerous conditions beforehand and undertake corresponding measures to eliminate them.

Fig. 6-54. Torsion break of a passenger car crankshaft made of GGG 70

The properties of the crank gear are therefore calculated in this regard. Since it is a complex system, the crank gear must be conceptually simplified (reduced) so that it can be computed with a reasonable amount of effort. The basis of such a simplification (reduction) is the harmonization of the dynamic properties of the reduced system with those of the actual system. The calculation of the rotational oscillation consists of

- Reducing the machine system
- Calculating the natural frequencies and modes of natural vibration
- Calculating the exciting forces and amplitudes
- Calculating the crankshaft excursions in the case of resonance
- Calculating the crankshaft stress from the vibration excursions in the case of resonance
- Calculating the critical speeds