Natural Frequencies and Modes of Natural Vibration
The crank gear consists of coupled moments of inertia and torsional rigidities with mutually influential vibration behavior. Movement equations are created for the individual moments of inertia.
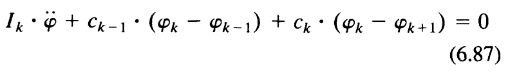

A system is obtained of homogeneously coupled linear differential equations with constant coefficients that describe the equilibrium between (Fig. 6-56)
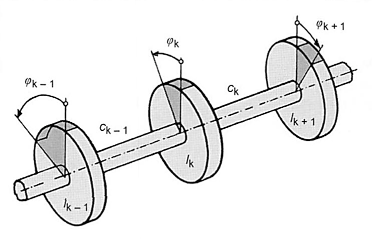
Fig. 6-56. Opposite rotation of the moments of inertia of the reduced crank gears
- Moments of acceleration from the moment of inertia arising from the inertial torque and the angular acceleration
- Returning torque from the spring rigidity and difference between the angles of twist on both sides of the examined mass.
The damping moment can be ignored when determining the natural frequencies since the natural frequencies are only slightly influenced by the damping when it is weak. The integration of these equations yields the natural frequencies of the system. To solve these differential equations, a model in the form of harmonic movement is created. Systems with more than three moments of inertia make the equation systems overly complex and difficult to deal with; for this reason, different experimental procedures have been developed. Of these, the procedure by Gümbel-Holzer-Tolle has gained broad acceptance. It provides insight into the physical behavior of the vibration processes and can be carried out using a simple and clear computational approach in which the results of one calculation step are used in the other as a pattern. The basic concept is as follows.
An oscillating torque is imagined that acts on the end of a system capable of vibration so that the system executes forced (undampened) vibrations; the amplitude of this oscillating torque (exciter moment amplitude) is set so that the vibration excursion of the first mass assumes the value 1. If the exciter frequency is then changed, the exciter moment M (residual exciter moment) also changes, which is necessary to maintain the vibration excursion 1 of the first mass. If the exciter frequency corresponds to one of the natural frequencies of the system, the amplitude Mk of the necessary exciter moment M is zero.

When doing the calculation, the residual exciter moment is calculated for the different exciter frequencies that are necessary to maintain vibration excursion 1 of the first mass, and the residual exciter moment is plotted over the exciter frequency. The intersections of the residual exciter moment curve with the abscissa yield the desired natural frequencies (Fig. 6-57).
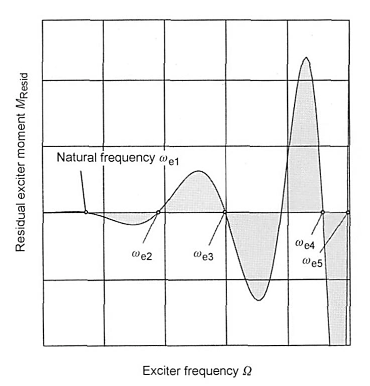
Fig. 6-57. Residual exciter moment curve
If the calculation is repeated with the natural frequencies found in this manner, we obtain the respective modes of natural oscillation ("Sum of the amplitudes of all moments of inertia that define the deformational state of the oscillating system for each frequency.") However, only the relative excursions, i.e., the excursions of the individual moments of inertia in reference to the excursion of the first moment of inertia (Fig. 6-58), are determined.
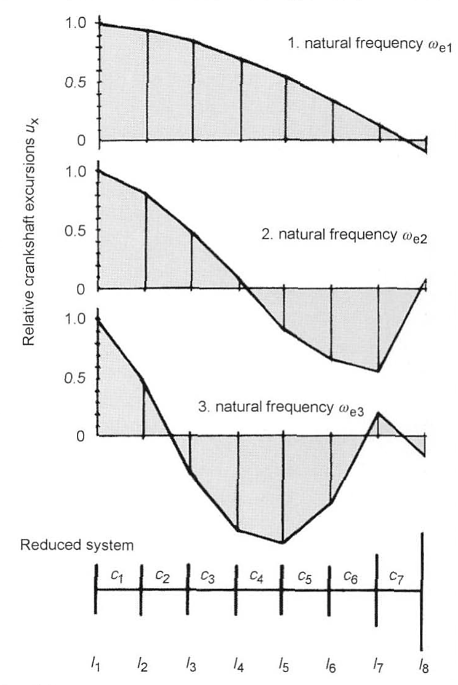
Fig. 6-58. Modes of natural oscillation for the three initial natural frequencies of a six-stroke crank gear with crank wheel and clutch
We are therefore dealing with a problem of intrinsic value whose solution is only for one common factor. To determine the absolute amplitudes, we need the exciting forces. Another solution corresponding to the Gümbel-Holzer-Tolle method is a matrix calculation. The relationships derived from the motion equations between the amplitudes of the rotational oscillation excursions and the return torques provide an equation system that can be represented with matrices and can be solved with a computer.
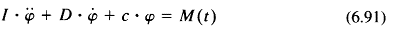
Date added: 2022-12-29; views: 662;
