Suspended and Tensioned Structures. Space Frames: Principles

The suspension or support of load-bearing structures provides a means of reducing the cross-sections of the structural members, thus enabling delicate and filigree designs to be developed. As a rule, this is only possible in steel and timber skeletal structures. The tensioning cables are of steel and can usually be tensioned on completion of the structure. The cables support tensile forces only.

Suspended structures have the purpose of reducing the span of supporting beams or eliminating cantilevered structures. Tensioned structures, likewise, reduce the span of beams and, hence, also the section modulus which has to be considered in determining their cross-section (12). In similar fashion to cable network structures, aerial supports are required on trussed structures. They have to accept buckling (compressive) stresses.

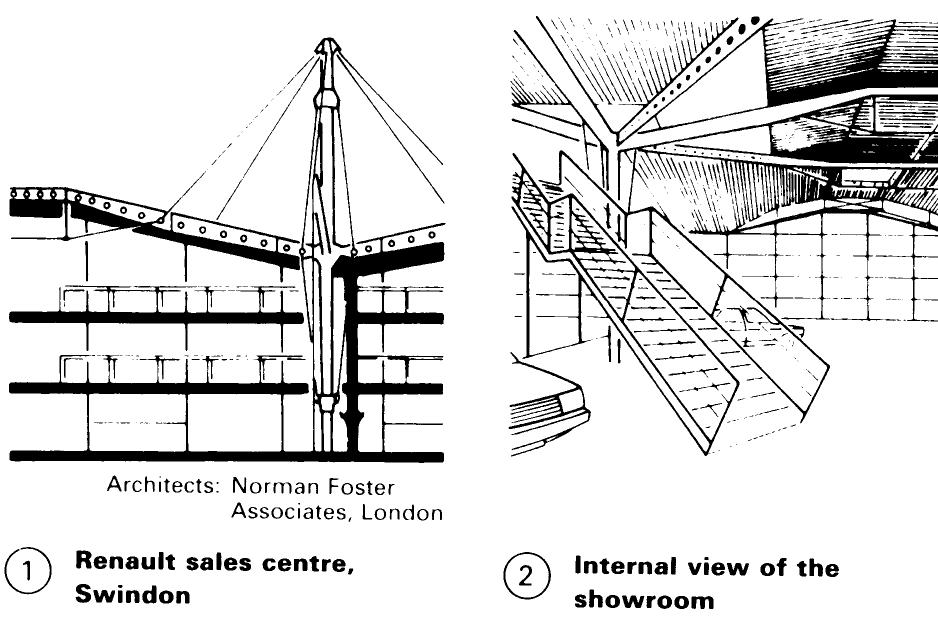
Significant contributions to the architecture of suspended structures have been made by Günter Behnisch – (5), Norman Foster – (1) – (4). Richard Rogers - (6) – (7) and Michael Hopkins – (8) - (9). The Renault building in Swindon, by Norman Foster, consists of arched steel supports, which are suspended from round, pre-stressed hollow steel masts from a point in the upper quarter of the gable – (1) - (4). The design enabled the ground area to be extended by approximately 67%. The suspended construction offers connection points which make it possible to execute the construction work without interfering with other work.

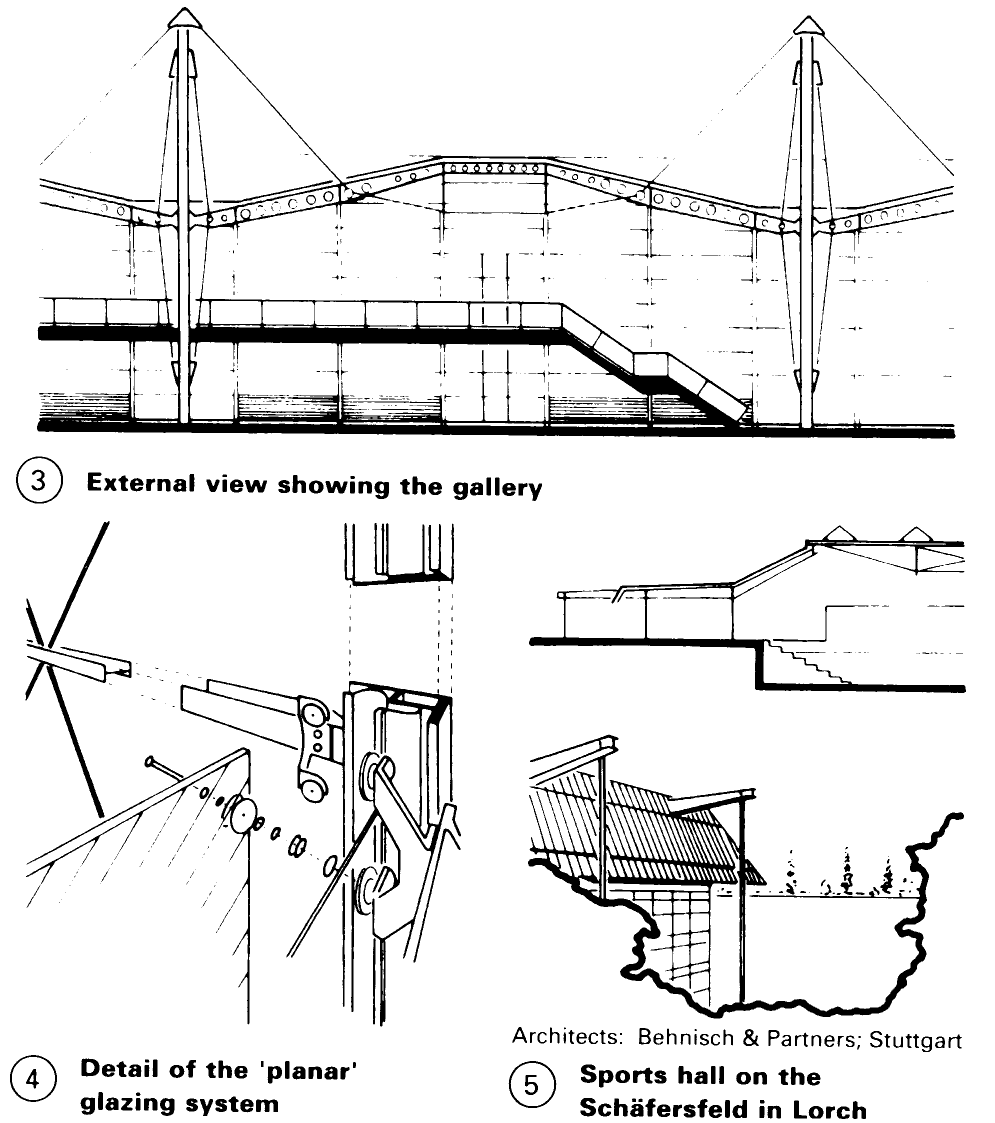
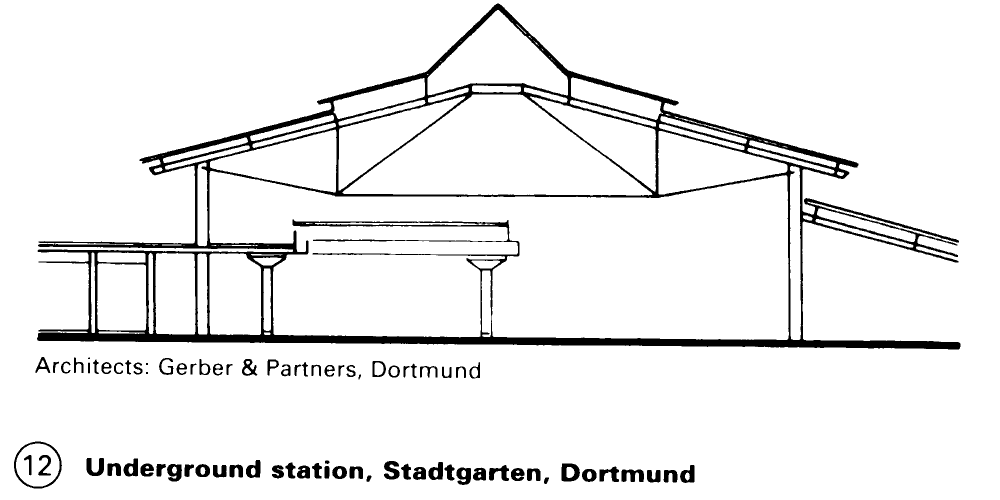
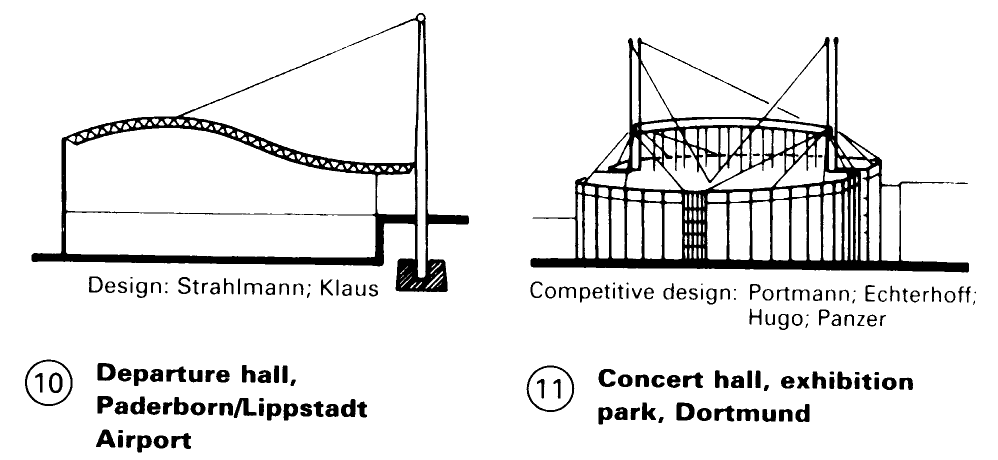
The new Fleetguard factory in Quimper, for an automobile concern in the USA, had to be designed for changing requirements and operations. For this, Richard Rogers chose a suspended construction so to keep the inside free of any supporting structure – (6) – (7). The same design ideas form the basis of the sports halls of Günter Behnisch - (5) and the Schlumberger Research Centre in Cambridge, by Michael Hopkins - (8) - (9). An airport administration building (proposed design for Paderborn/Lippstadt) – (10) and a concert hall (proposed design for the Dortmund Fair) (11) may also be built in this fashion.

Space Frames: Principles. Ideally, space frames should be constructed from equal sided and/or isosceles right-angled triangles, so that regular polyhedrons are formed. In plane infinite networks, there are exactly three geometric structures; in spherical finite structures, there are exactly five regular polyhedron networks, which are comprised of only one type of joint, member, and hence also, surface. Regular plane networks are triangular, square and hexagonal.

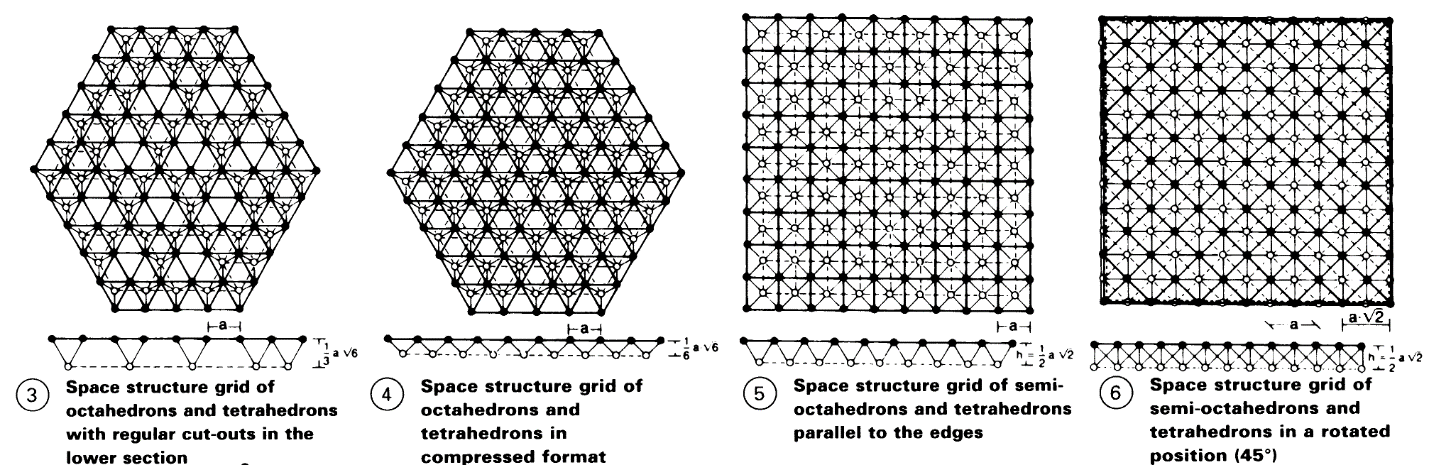
Of the five platonic bodies used, the space frame formula decrees that only those three-dimensional joint-member space frames whose members form a closed triangular network are kinematically stable, i.e. the tetrahedron, the octahedron and the icosahedron. The cube requires an additional 6, and the dodecahedron, an additional 24 members, to become stable. If a spherical, triangular network is not closed over the whole surface, the basic polygon must be prevented from moving by an appropriate alternative method.

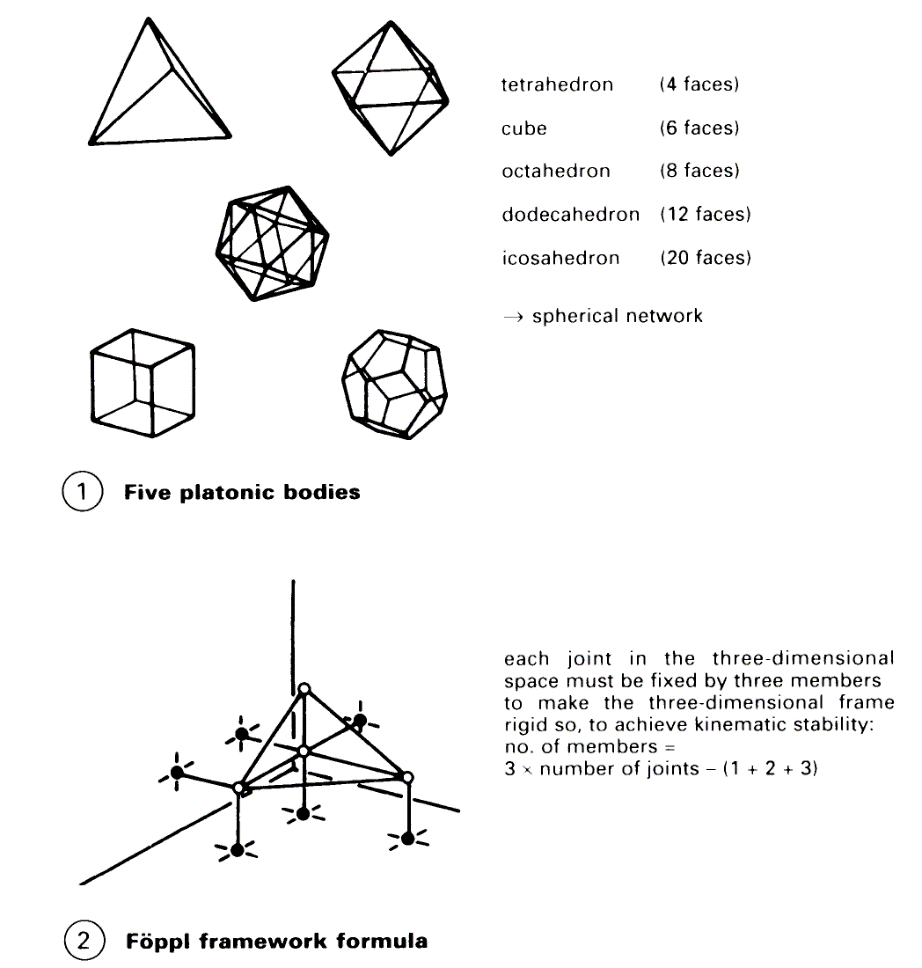
The lengths of the members of a body for a space frame form a geometric series with the factor 2. One joint with a maximum of 18 connections at angles of 45°, 60° and 90° is sufficient for the construction of a regular framework. As with plane structures, it must be accepted that the members are connected with flexible joints.