Robot Motion Planning. Workspace and Configuration Space
The aim in robot motion planning is to be able to specify a task in a high-level, expressive language and have the robot(s) automatically convert the specification into a set of low-level primitives, such as feedback controllers and communication protocols, to accomplish the task (1,2).
The robots can vary from manipulator arms used in manufacturing or surgery, to autonomous vehicles used in search and rescue or in planetary exploration, and to smart wheelchairs for disabled people. They are subject to mechanical constraints (e.g., a car-like robot cannot move sideways and an airplane cannot stop in place) and have limited computation, sensing, and communication capabilities.
The environments can be cluttered with possibly moving and shapechanging obstacles and can contain dynamic (moving, appearing, or disappearing) targets. The challenge in this area is the development of a computationally efficient framework accommodating both the robot constraints and the complexity of the environment, while allowing for a large spectrum of task specifications.
A robot combines moving mechanical pieces such as wheels, gears, and breaks with digital devices such as processors and sensing and communication devices, in continuous interaction with a possibly changing environment.
Therefore, motion planning is a highly interdisciplinary area, combining tools from computer science, mechanics, control theory, and differential geometry. Given the variety of applications, many motion planning approaches have been developed over the years. Depending on the task they address, motion planning problems can roughly be divided into four main groups: navigation, coverage, mapping, and localization(3).
In navigation, the problem is to find a collision-free motion between two configurations of the robot. Coverage is the problem of moving a robot sensor or end effector in such as way that it reaches all points in a target space (e.g., painting a surface). Mapping involves exploring an environment with the goal of producing a representation that can be used, for example, in navigation and coverage. Finally, in localization, the problem is to use a map and sensor data to determine the configuration (state) of the robot. Localization and mapping are sometimes performed simultaneously, such as in simultaneous localization and mapping (SLAM)(4).
Motion planners also differ depending on the robot model they consider. For example, it is much easier to plan the motion of a robot that is free to move instantaneously in all directions of its configuration space (omnidirectional robot), rather than generating motion for a carlike or an airplane-like vehicle that cannot move sideways (i.e., nonholonomic robot; see Ref. 5 for a collection of motion planning approaches for such robots). Motion planning can be performed for kinematic robot models, which capture only the configuration and velocity of the robot, or for dynamic robot models, which capture forces and accelerations.
Motion planning approaches can also be classified depending on the properties of the underlying algorithms. A motion plan is optimal if the produced motion minimizes energy consumption, execution time, trajectory length, and so on. Computational complexity is also a determining factor. For example, in most cases, it is desired that the amount of necessary memory and running time scale polynomially with the size of the input of the planner, which can be the number of obstacles, the number of degrees of freedom of the robot, and so on.
Finally, a planner is complete if it always finds a path if one exists. Others are resolution complete, if a solution is found whenever one exists at a given discretization resolution, or probabilistic complete, if the probability of finding a solution during an iterative discretization process converges to 1 when the solution exists.
Workspace and Configuration Space. Given a robotic system, a configuration is a complete description that determines the position of every point of the system uniquely. Its configuration space, called for simplicity C-space, is the set of all possible configurations of the system. The number of degrees of freedom of a robotic system is the dimension of its minimal configuration space or, in other words, the minimum number of parameters needed to describe the system completely.
The space in which the robotic system does work is called the workspace, which can be seen as the Euclidean space R2 or R3, depending on whether the motion is in plane or space. Most often, however, the workspace is defined more precisely as the subset of R2 or R3 that can be reached by a point of interest on the robot, such as the end effector of a manipulator arm.
Consider, for example, a two-joint planar robot arm, where a point on the first link is pinned to the ground, and the base of the second link is pinned to the end of the first, such that the only possible motion of the second link is a rotation about the (revolute) joint [Fig. 1 (a)].
If we denote by 01 and 02 the angles formed by the two links with the horizontal, then (01, 02) can be seen as coordinates of the configuration space, which is S1 x S1 = T2, where S1 and T2 denote the unit circle and the torus, respectively [Fig. 1 (c)]. The workspace of this robot, however, is an annulus, with the outer radius determined by the sum of the lengths of the two links, and the inner radius is given by the difference between their lengths [Fig. 1 (b)].
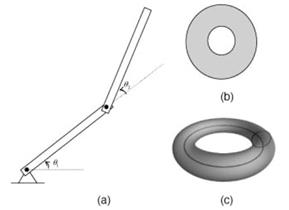
Figure 1. A two-link manipulator (a), its workspace (b), and its configuration space (c)
The configuration space of a planar square robot (or any other rigid body) that can only translate without rotation (see Fig. 2) is R2. For a planar robot that can only rotate about a fixed point, the configuration space is SO (2), called the Special Orthogonal group in the plane, which is isomorphic to S1. The configuration space of a robot allowed to translate and rotate in the plane is SE(2), called the Special Euclidean group in the plane, and defined as SE(2) = R2 x SO (2). In space, a rotating and translating robot modeled as a rigid body evolves in SE(3) = R3 x SO(3), where SO(3) is the group of rotations in space (3).
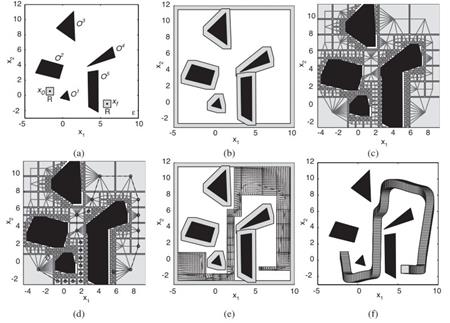
Figure 2. Cell decomposition and simultaneous planning and control for a square robot translating (no rotation) in a 2-D rectangular environment with polyhedral obstacles. The observable is the centroid of the robot: (a) initial (left) and final (right) positions of the robot. (b) The free C-space is obtained by enlarging the obstacles, shrinking the environment boundaries, and reducing the robot to its observable point.
(c) Rectangular (quadtree) partition of the free C-space and the quotient graph of the partition. (d) Optimal path from initial to final node (rectangle) in the quotient graph; and X denote the initial and final position of the robot observable, respectively. (e) Vector field assignment (used in simultaneous planning and control) and the resulting trajectory of the observable. (f) Robot motion in the initial environment
If obstacles are present in the workspace, it is useful to define explicitly the set of robot configurations for which collisions occur. For each obstacle in the workspace, the configuration space obstacle is defined as the set of all configurations at which the robot intersects the obstacle in the workspace. The free configuration space, also called free C-space, is the set of configurations at which the robot does not intersect any obstacle.
Figure 2 (b) shows the free C-space for the square robot moving in the environment shown in Fig. 2 (a), if only translational motion is allowed (no rotation). The reader is referred to Ref. 3, p. 509 for an example of the free C-space construction for a polytopal robot translating and rotating in a polytopal environment with polytopal obstacles. In this setup, a navigation problem, as defined above, translates to finding a continuous curve between the initial and the final configuration in the free C-space.
Date added: 2024-02-27; views: 534;
