The membrane potential. Ohm's law

The plasma membrane has different types of integral proteins (Figure 2.1), defined as ion channels, which allow the passage of charged particles. When the cell is at rest, it is in a dynamic equilibrium.

The value of the membrane potential is determined by averaging the Nernst potentials for each permeable ion multiplied by its permeability. Generally speaking, the main basic conductance that influences the resting membrane potential is due to potassium ions. However, often the membrane potential values reflect the function that a particular cell is called on to accomplish.

Because potassium permeability is essentially ubiquitous, the range of membrane potentials spans from the potassium equilibrium potential and the average between potassium and sodium reversal potentials. This value is between -15 and -20 millivolts.

There is actually continuous leakage of potassium, which tends to bring the difference in electrical potential across the membrane, the resting membrane potential, towards its equilibrium potential. In fact, we have seen how the escape of an ion by the chemical gradient proceeds until the electric potential generated reaches the value of the ion's equilibrium potential.

To measure the membrane potential of a cell, an experimental apparatus used is the voltmeter. A microelectrode (Data Sheet 3.4) is moved with a micromanipulator until it touches the plasma membrane and perforates it. Due to its fluidity, the plasma membrane closes and seals itself on the capillary glass.

The microelectrode (Figure 3.19) is connected to the positive input of the voltmeter (In⁺), while the electrode placed in the extracellular solution, or reference electrode, is connected to the negative input of the same voltmeter (In^-). The voltmeter (Vo) measures the differences in potential between the inside of the cell (V_m) and the outside (V0). It is convenient to set the external potential equal to zero by connecting the input In- of the voltmeter to ground (reference electrode).

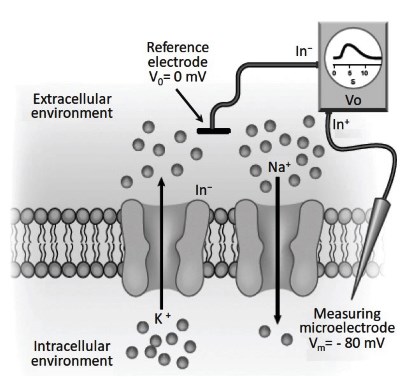
Figure 3.19. Using a glass microelectrode filled with a concentrated KCl solution and a voltmeter (Vo), the membrane potential can be measured

To identify the electrical energy content of a cell, the correct term is "the potential difference across the membrane". Conventionally, the external reference electrode is connected to ground at zero voltage. This allows discussion of "cell membrane potential" instead of "difference in potential between the inside and outside of the membranes".

The microelectrode is unlikely to be positioned close to the membrane, as shown in Figure 3.19, but more probably towards the center of the cell. Nevertheless, it senses the potential in the immediate proximity of the membrane where is actually generated (Figures 3.17-3.18).

To set the resting membrane potential, the main contribution comes from potassium and sodium permeability. However, all of the ions present on both sides of the membrane, chloride, calcium, etc., can influence the resting membrane potential if they can move across the membrane. Lastly, the mechanism of maintaining stability in the resting membrane potential is recharging through the continuous work of the electrogenic active Na/K ATPase (Figure 3.15).

A complete mathematical description of the cell membrane potential is given by the Goldmann equation.

The Goldmann equation. The Goldmann equation, which is derived directly from the Nernst equation (Equation 3.1), relates the membrane potential Vm to the concentration and permeability of the ions exchanged by the cell at rest (potassium, sodium and chloride):

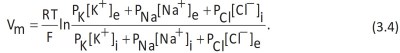
Given a temperature of 18 °C (291 K), known R and F values (Data Sheet 3.2) and when the cell is not undergoing any kind of stimulation, the sodium and chloride to potassium permeability ratios are according to the proportion

It follows that the membrane potential of the cell at rest with an ion distribution such as that in Table 3.2, or resting potential, will be:

like that measured experimentally (paragraph 3.5).

Ohm's law. The electric circuit in Figure 3.18 represents the plasma membrane. A charge passing through a resistor is a current which depends on the potential difference according to Ohm's law:

in which the current I expressed in amperes (A) is proportional to the voltage V expressed in volts (V) and the proportionality constant is the reciprocal of the resistance R expressed in ohms (Ω) or the conductance G expressed in Siemens (S).

If we consider the cell, the current (given by the ion I crossing the plasma membrane using its ion channels) is proportional to the difference between the membrane potential V_m and the equilibrium potential of the ion I E_i, since this influences, as we have seen, the movement of the ions across the membrane, according to the relationship that is normally called generalized Ohm's law

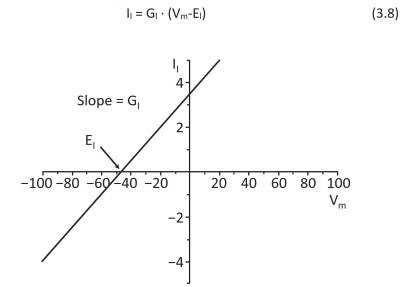
Figure 3.20. Equation 3.8 represents a straight line with slope G_I and zero current when V_m=E_I. V_m is expressed in mV (V_I • 10^-3) and I_I in pA (A • 10^-12)

conductance G_i for ion I. The difference between the membrane potential V_m and the equilibrium potential E_i of ion I is generally called the electromotive force (e.m.f.) or driving force. From Equation 3.8, which in a current-voltage graph represents a straight line with slope GI crossing the x-axis when V_m = E_I (Figure 3.20), it can be deduced that I_i is constant if V_m is constant and varies when V_m varies, but in turn varies V_m.

Moreover, if V_m becomes equal to E_I, the current becomes, as observed above, equal to zero and the channels must be open, i.e., the conductance must be greater than zero, since a current has passed that has made V_m vary. It will be seen later that the conductance, in many cases, also depends on V_m.

Bibliography: Nutman A, Bennett V, Friend C, Van Kranendonk M, Chivas A. Rapid emergence of life shown by discovery of 3,700-million-year-old microbial structures. Nature (2016) 537(7621): 535–538. Neil A Campbell NA and Reece JB., Meccanismi dell'evoluzione ed origini della diversità. Zanichelli 2004.