Simple diffusion. Diffusion in the presence of a membrane

Diffusion is a mechanism which, by exploiting the mobility of the molecules due to thermal agitation, allows the movement of substances without the consumption of chemical energy. Diffusion can take place between two points in the same environment, such as a solution.

Aqueous environment is the physical substrate from every "fast" chemical reaction because indeed medium is dynamic and allows mobility of molecules that a solid state would not. It also occurs between two environments separated by a biological membrane, provided there are aqueous pores.

Diffusion always occurs according to a gradient, i.e., from the environment with the highest concentration to that with the lowest concentration.

Simple diffusion. The mechanism by which a molecule can move from one point to another in an aqueous environment is that of simple diffusion, which, for example, allows dye deposited in a well-defined area of a container to invade the entire environment.

To analyze this phenomenon, suppose we have a drop of water-soluble dye in a container containing distilled water (Figure 4.1). In the area where the drop is deposited, there is a high concentration of dye. In the surrounding area, it is the water with a high concentration (Figure 4.1A).

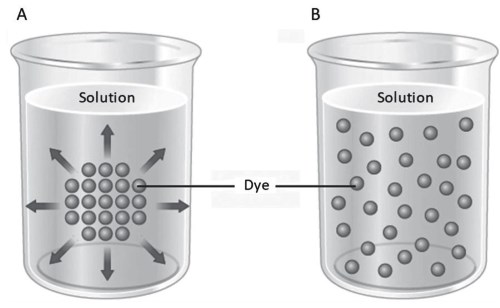
Figure 4.1. The dye deposited at one point in the vessel diffuses homogeneously into the solution

Each molecule has kinetic energy proportional to its temperature. As long as it is above absolute zero (-273 °C), molecules continuously move by thermal agitation in uniform rectilinear motion, in a random direction in space, in a temperature-dependent manner. A change in direction occurs because one molecule hits another. Initially, water and dye are at high concentrations: it is highly probable that a molecule of dye will move from the drop of dye to the water, as well as a molecule of water moving from the water to the drop of dye, but the probability of opposite movements

is practically null. If we define by Φ_1-2 the unidirectional flow of the dye through the entire outer surface of the drop towards the water and by Φ_2-1 the unidirectional flow in the opposite direction, the net flow Φ_n will be given by the equation:

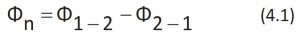
At the beginning of the process, the Φ_1-2 flow of dye from the drop to the water will be maximum due to the large difference in concentration between the drop and the water. The Φ_2-1 flow of dye from the water to the drop will be zero as the concentration of dye in the water is zero. Therefore, according to equation 4.1 the net flow Φ_n will be equal to Φ_1-2.

A time course of the bidirectional flux shows a decrease of intensity in the Φ_1-2 flow and a related increase in the flow Φ_2-1 as the concentration of the dye increases in the water and decreases in the drop. Consequently, the probability that a new dye molecule can pass into the water and that a water molecule can pass into the drop of dye decreases. This phenomenon affects all the molecules of dye and water present in the container, until an equilibrium is reached so that the unidirectional flow Φ_1-2 will be equal to the unidirectional flow Φ_2-1 (Figure 4.1B).

Diffusion is thus proportional to the difference in concentration of the dye but also of the solvent, in this case water. A mechanism similar to the one just described can be assumed in a situation such as that depicted in Figure 4.2A.

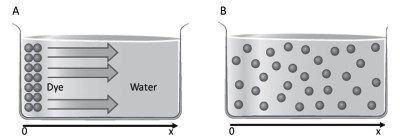
Figure 4.2. The dye diffuses into the solution (A). Only at the final time t4 (Figure S4.1) is the concentration homogeneous (B)

Due to the diffusion phenomenon, the dye, deposited at the point close to x=0 and with the same concentration in the whole area, will move until it is homogeneously distributed throughout the cylinder (Figure 4.2B). The flux Φ, i.e., the number of moles dn moving in the time unit dt, dn/dt, across the region A is given by Fick's law of simple diffusion of an apolar molecule (Data sheet 4.1):

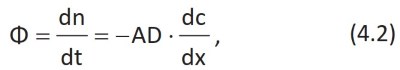
and is proportional to the concentration gradient according to the constant D, which is the diffusion coefficient and has the dimensions of a velocity x length.

Fick's law describes the flow of any apolar molecule in any solution because D is typical of each substance. The driving force for the diffusion process is exclusively the concentration gradient both of the solute and of the solvent.

Diffusion in the presence of a membrane. In a cylinder (Figure 4.3), a membrane of thickness X and area Am separates environment 1, in which the water-soluble substance S is present at concentration C_S1, from environment 2, in which the concentration of S, C_S2, is initially zero (Figure 4.3A). The passage of S across the plasma membrane from environment 1, e.g., the outside of a cell, to environment 2, the inside of a cell, is indispensable for the cell.

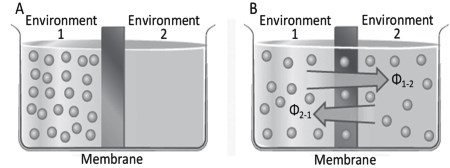
Figure 4.3. Diffusion in the presence of a membrane

If S can diffuse freely across the membrane and if we assume that its diffusion coefficient DS is sufficiently large and is equal in the two environments, we will have a net flux Φ_nS according to Equation 4.1 (Figure 4.3B). This flux tends to decrease in time until it is exhausted because each unidirectional flow is proportional to the difference in concentration between the two environments C_S1 and C_S2 and this varies in time. As C_S1 decreases, C_S2 increases, reaching an equilibrium in concentration between the two environments (Figure 4.4).

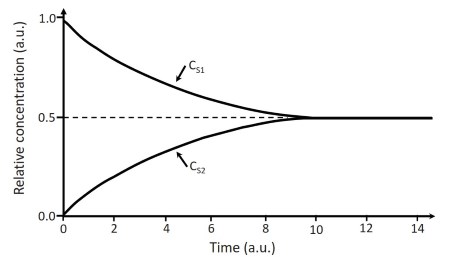
Figure 4.4. Relative concentration trend at time t=0 in environment 1 (C_S1) and environment 2 (C_S2)

The equation describing the net flux of substance S per unit area A, J_nS, is derived from Fick's law, in which the difference in concentration between environments 1 and 2 is considered (Figure 4.2):

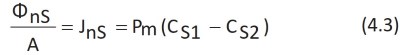
Pm is the permeability coefficient of S in the membrane, is proportional to the membrane diffusion coefficient D_m and is the size of a velocity.

By measuring J_nS with flow measurement experiments and knowing C_S1 and C_S2, one can derive P_m in different biological membranes for various substances of physiological interest.

P_m varies greatly for different molecules crossing membranes of different cells. For example, in erythrocytes, it can vary from 1 · 10^-12 to 1 · 10^-2 cm/s. In addition, this parameter can be modified by the action of various substances through specific membrane receptors.

An example is the case of antidiuretic hormone, which can make the nephron's collecting ducts up to 10 times more permeable to water. Other examples are several neurotransmitters that can increase the membrane ionic permeability of the target cell.