Topographic Slopes and Solar Radiation: Shaping Local Microclimates

Local and regional climates can deviate from the broad macroscale geography of solar radiation based on topography. The direct beam radiation on a sloped surface depends on the Sun’s zenith angle, the angle of slope, the direction of the Sun, and the direction of the sloping surface (Figure 4.10). A surface receives maximum intensity when it is oriented perpendicular to the Sun’s rays. On a sloped surface, the angular deviation from perpendicular must be adjusted for the tilt of the surface. The incidence angle is the angle between the Sun’s beam and an imaginary line perpendicular to the slope. This angle is:

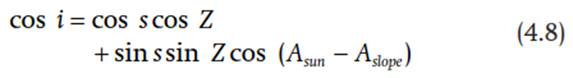
where s is the angle of slope and A_slope is the azimuth of the slope. The azimuth angle of the slope is the compass direction to which the slope is oriented (e.g., north = 0°, east = 90°, south = 180°, west = 270°). The direct beam radiation onto the surface is:

On a horizontal surface, s = 0° and the incidence angle is the zenith angle. On a sloped surface, the incidence angle can be more or less than the zenith angle depending on the angle and orientation of the slope.

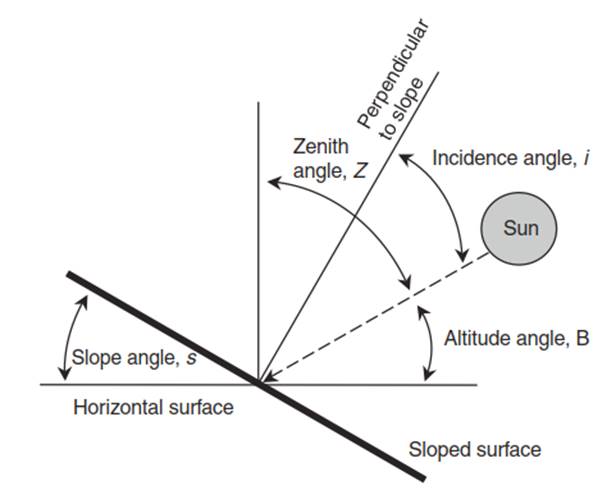
Fig. 4.10. Altitude, zenith, and incidence angles for a sloped surface

The diffuse radiation on a sloped surface also depends on the angle of slope. The sky forms an inverted bowl, or half sphere, above and around a point in the landscape (Figure 4.11). On a horizontal surface, diffuse radiation emanates from all portions of the sky. As the surface tilts at an angle, less of the sky hemisphere is viewed from a point on the surface. The terrain blocks a portion of the sky, from which no sky diffuse radiation is received. With a vertical wall, the sky hemisphere is cut in half and each side of the wall receives diffuse radiation from only one-half of the sky. A sloped surface, therefore, sees less of the sky as the angle of slope increases. The fraction of the sky seen, known as the sky view factor, is given by:

The portion of the sky that is not blocked, (1 - ψ_sky), is the fraction of the hemisphere composed of terrain. This terrain is also a source of diffuse radiation, because some of the solar radiation incident on the slope is reflected. As the angle of slope increases, less of the sky contributes diffuse radiation and more of the terrain is viewed.

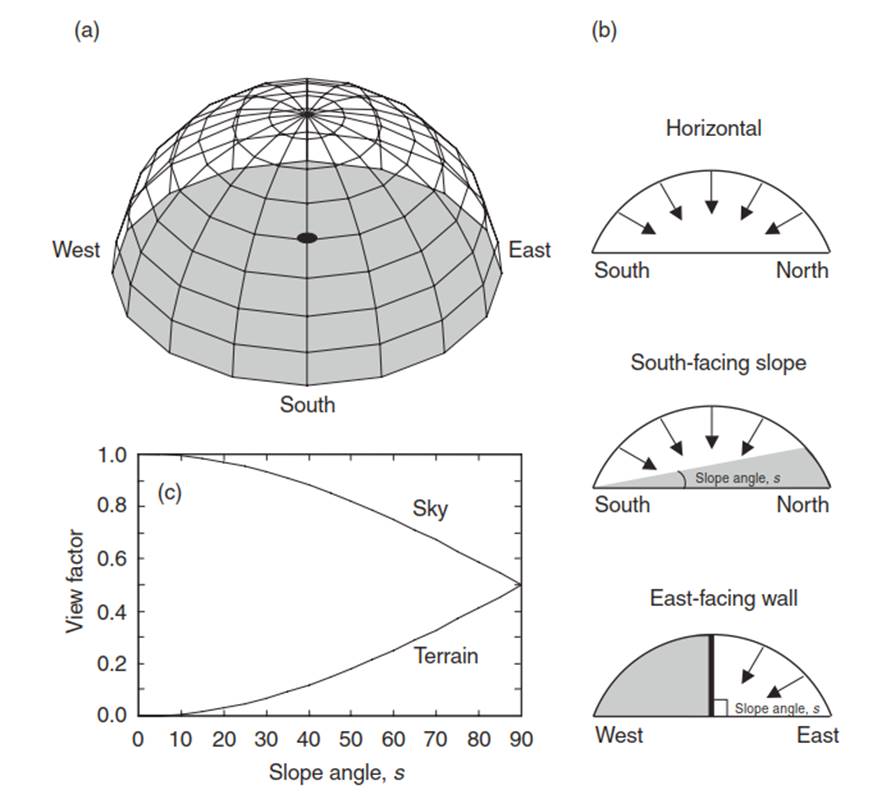
Fig. 4.11. Effect of angle of slope on diffuse radiation. (a) The sky is shown as an inverted bowl, or hemisphere, from which diffuse radiation is received. The point in the center receives diffuse radiation from the entire hemisphere. (b) The three right-hand panels show a cross-section of this hemisphere for a horizontal surface, a south-facing slope, and a wall. The gray area is the portion of the sky that is blocked. (c) Sky and terrain view factors in relation to angle of slope

Figure 4.12 illustrates direct and diffuse radiation on various slopes, ignoring terrain radiation. For all diagrams, the Sun is due south with a zenith angle of 27° (63° elevation above the horizon). On the 27° (51%) south-facing slope, a line perpendicular to the slope is oriented 63° above the horizon. This is the same angle at which the solar beam strikes the surface so that the incidence angle is 0° and the surface receives 100 percent of the direct beam radiation. The surface receives diffuse radiation from 95 percent of the sky. On the 27° north-facing slope, diffuse radiation is still received from 95 percent of the sky. Now, however, the solar beam strikes the surface at an angle of 54° from local perpendicular, and the direct beam radiation is only 59 percent. A greater portion of the sky is blocked on the 45° (100%) slopes; the surfaces receive diffuse radiation from only 85 percent of the sky. Both 45° slopes receive less direct beam radiation than the comparable 27° slopes.

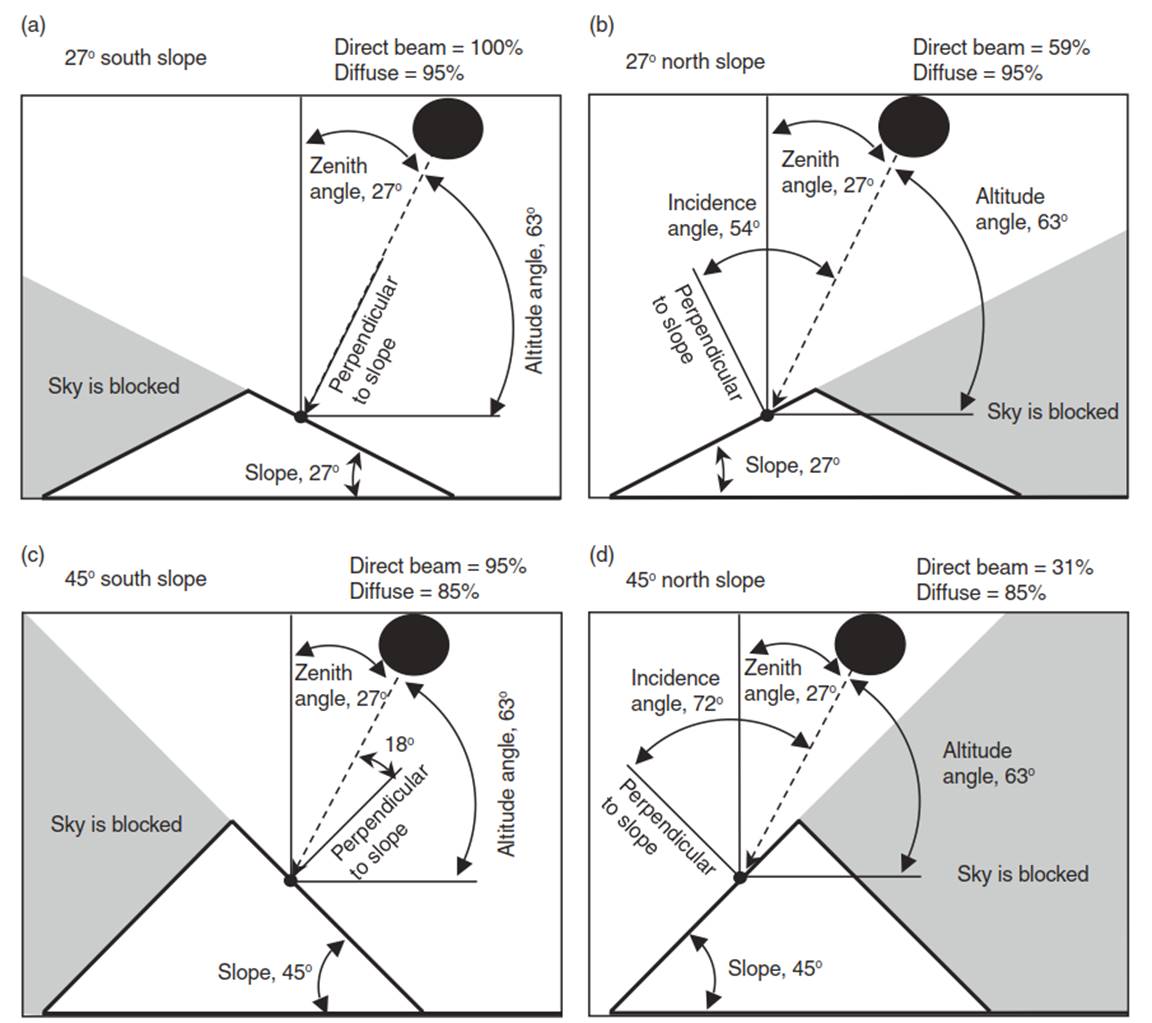
Fig. 4.12. Direct beam and diffuse solar radiation on slopes. In all four panels, the Sun is due south with a zenith angle of 27°. Direct beam radiation varies with angle of slope and aspect in relation to incidence angle. Shown is the percentage of perpendicular radiation. The portion of the sky from which diffuse radiation is received varies with the angle of slope, given as a percentage of sky radiation. (a) 27° south-facing slope. (b) 27° north-facing slope. (c) 45° south-facing slope. (d) 45° north-facing slope

The incidence angle on the south-facing slope is 18° while that of the north-facing slope is 72°. In these examples, angle of slope has little effect on diffuse radiation. The greatest reduction in diffuse radiation from horizontal is only 15 percent. Angle of slope has relatively minor effect on direct beam radiation for the south-facing slopes. The greatest reduction in radiation comes from the direction of slope. The 27° north-facing slope receives only 59 percent of the direct beam radiation on the south-facing slope. The 45° north-facing slope receives one-third of the direct beam radiation of the south-facing slope.

The angle of slope, its direction of tilt, and latitude interact with time of year and time of day to produce complex patterns of solar radiation on a surface.

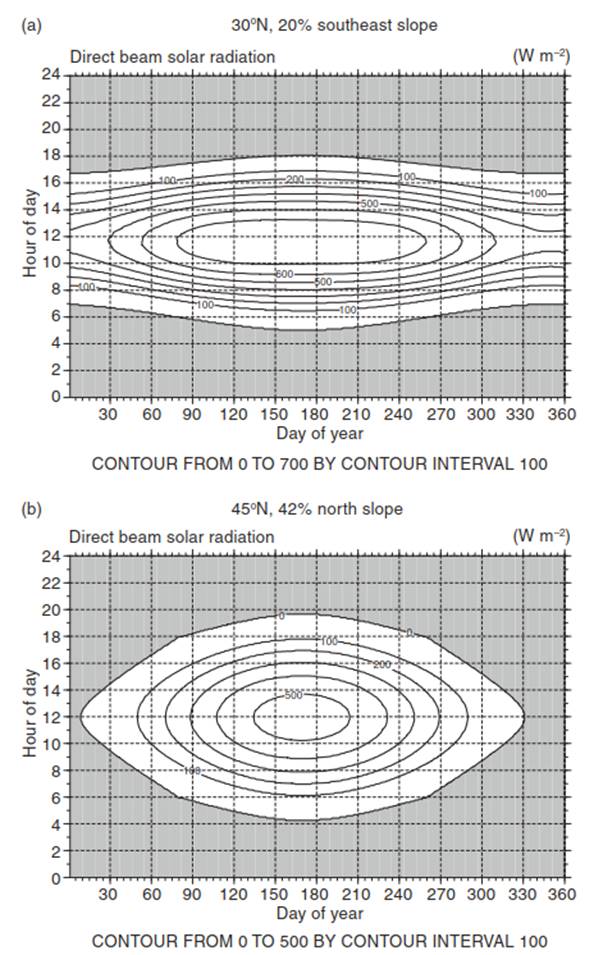
Fig. 4.13. Clear sky direct beam solar radiation as a function of time of day (vertical axis) and day of year from January 1 to December 31 (horizontal axis) for (a) a 20 percent southeast slope at latitude 30° N and (b) a 42 percent north slope at latitude 45° N. Direct beam radiation is from eq. (4.9) with τ = 0.6

Figure 4.13 shows the diurnal pattern of direct beam radiation throughout the year on a 20 percent (11°) southeast slope located at latitude 30 °N and a 42 percent (23°) north slope at latitude 45 °N. Noon direct beam radiation is relatively constant throughout the year on the southeast slope, but varies greatly throughout the year on the north slope. The length of day the solar beam illuminates the slope varies by less than three hours over the year on the southeast slope. In contrast, the north slope receives no direct beam radiation from December to mid-January, and daylength increases to 15 hours in June. This topographic variation in solar radiation can create unique microclimates with the general macroclimate.