The Utilitarian Roots and Development of Early Mathematical Systems

The emergence of mathematical methods was inextricably linked to the rise of writing, stemming from identical practical necessities of early state administration. As noted by the ancient Greek historian Herodotus, the origins of geometry—literally "earth measure"—in Egypt were tied to the annual need to resurvey farmland after the Nile River's floods. Similarly, the management of agricultural surpluses from irrigation agriculture necessitated standardized systems for trade and taxation, leading to the first money in Babylonia and Shang China, and the first standardized weights and measures in Egypt, the Indus Valley, and China. While later Greek thinkers refined mathematics into an abstract discipline, its foundations remain firmly rooted in these economic and administrative applications.

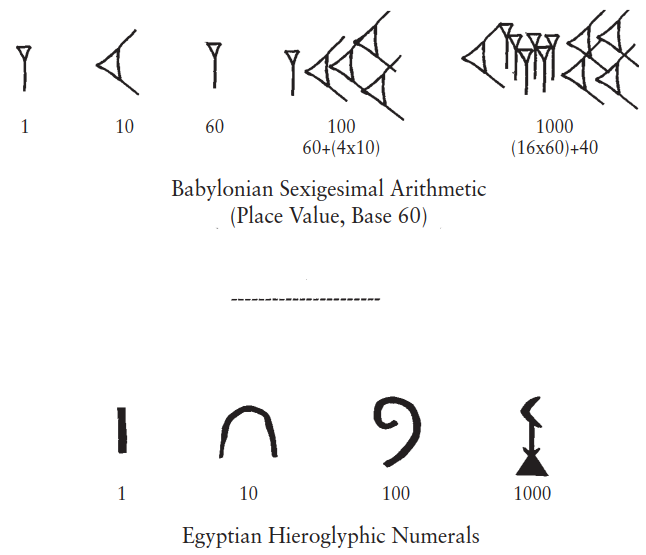
Fig. 3.6. Babylonian and Egyptian number systems. Different civilizations developed different numeral systems and reckoning methods. The Babylonian system was a base-60, place- value system with number signs for the values 1 and 10. Egyptian hieroglyphic numerals represented values of 10 in a manner reminiscent of later Roman numerals. No civilization was without a system to record numerical information.

Each primary civilization developed a distinct numerical system tailored to its needs. The ancient Sumerians and Babylonians created a sophisticated sexigesimal or base-60 system, which was the world's first place-value system where a digit's value depended on its position. Though it initially lacked a true zero and was not perfectly consistent, its legacy endures in our modern 60-minute hour, 60-second minute, and 360-degree circle. In contrast, the Egyptian number system functioned more like later Roman numerals, utilizing separate signs for units, tens, and hundreds without a place-value concept. This rendered it more cumbersome for complex calculation, yet it still effectively managed the state's logistical requirements.

Regarding mathematical operations, Babylonian mathematicians employed extensive tables of multiples, reciprocals, squares, and Pythagorean triplets to perform advanced calculations. Their procedural, recipe-like methods could solve problems involving compound interest and find solutions to what we recognize as quadratic and cubic equations. Egyptian calculators, using a "method of duplication" (doubling and halving), adeptly multiplied numbers within their less-efficient notational system. They achieved a superior approximation of pi (π) at 256/81 (≈3.16) and developed sophisticated techniques for handling unit fractions, as documented in texts like the Rhind Mathematical Papyrus.

The problems addressed by these early mathematicians consistently reflect a utilitarian focus, centered on engineering, supply logistics, and land division. Solutions were typically expressed as step-by-step algorithms or "recipes," providing correct computational answers without recourse to generalized theorems or abstract proofs. This approach is analogous to following a cooking recipe or executing a computer program that applies an underlying formula without explaining its derivation. The primary goal was reliable, repeatable results for state projects, not theoretical exploration.

Nevertheless, within this overwhelmingly practical framework, glimpses of esoteric intellectual "playfulness" occasionally surfaced. Babylonian scholars computed the square root of 2 to an astonishing accuracy of six decimal places, far beyond any practical need. Likewise, later Chinese mathematicians pursued extreme precision in calculating pi. However, even these seemingly abstract pursuits typically developed within broader utilitarian contexts; for instance, Babylonian tables of exponential functions were used for financial calculations, and solutions to quadratic equations arose from land division problems. The computation of volumes and areas directly applied to constructing canals, granaries, and monuments, demonstrating that utilitarian mathematics served as the essential cradle for all later mathematical thought.