PH Scale. Strong Bases

Although samples of pure water are in principle neutral and contain equal concentrations of H₃O⁺ and OH^- ions (1.0 x 10^-7M), it is essentially impossible to find (or generate) samples of molecularly pure water. It is natural and common for water to contain solutes that can cause the concentrations of H₃O+ and OH^- ions to deviate from balanced values of 1.0 x 10^-7 M.

Over time, scientists learned that they can systematically manipulate aqueous solutions by adding solutes known as acids and bases in controlled concentrations. These solutes can be used to cause the concentrations of H₃O+ (and OH^-) ions to vary over many orders of magnitude. The parameter pH (Eq. (3)) was developed to provide a convenient logarithmic index for expressing H₃O+ ion concentrations.

pH = -log[H₃O⁺] (3)

It was also natural for the parallel parameter pOH (Eq. (4)) to be defined.

pOH = -log[OH^-] (4)

It can be easily shown (by taking the negative logarithm of both sides of Eq. (1) that pH and pOH have a simple relationship with each other (Eq. (5)). They must always add to 14 in any aqueous solution. In a more rigorous treatment we would distinguish between the p^aH and the p^cH corresponding to the activity- and concentration-derived pH values. This goes beyond the scope of the present article, so we will assume that pH is the same as p^cH from now on.

pH + pOH = 14 (5)

Figure 4 illustrates the typical “pH scale," which ranges from 0 to 14. This pH range corresponds to H₃O+ concentrations that continuously vary from 1.0 to 1.0 X10^-14 molL^-1 and OH^- concentrations that simultaneously range from 1.0X10^-14 to 1.0molL^-1. (Between 0.01 and 1.0 M, the concentration deviates from the activity from 10% to 20% for HCl. However, this translates into an error in the pH that ranges respectively from 0.04 to 0.1 pH units, an error that is insignificant for the purposes of this article.)

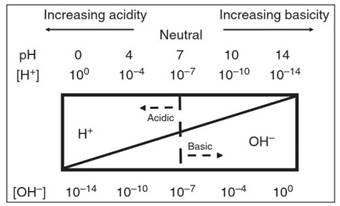
Figure 4. A depiction of the common pH scale used to describe the acid-base condition of aqueous solutions which vary in their relative concentrations of H+ (or H₃O+) andOH^- ions

The center of the pH scale is seven, and solutions can be caused to depart from neutrality by negative or positive changes in pH caused, respectively, by the addition of acids or bases to the solution. In “acidic" (pH <7) solutions, the concentration of hydronium ions exceeds that of hydroxide ions (i.e. [H₃O+] > [OH^-]), and in “basic" (pH >7) solutions, the concentration of hydroxide ions exceeds that of hydronium ions (i.e. [OH^-] > [H₃O+]).

It is hence seen that the relative acidity (or conversely basicity) of aqueous solutions can be described using any of the four parameters [H₃O+], [OH^-], pH, or pOH. The values of these four parameters are clearly interrelated; specification of any one of the parameters “locks" the other three into straightforwardly calculated values, as summarized in Figure 5.

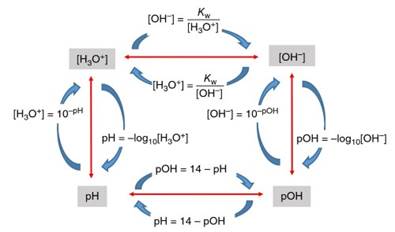
Figure 5. Relationships between the parameters ([H₃O⁺], [OH^-], pH and pOH) used to describe the acid-base conditions of aqueous solutions

Sample calculation: (a) A solution has [H₃O+] = 4.53 X 10^-9M. Calculate the parameters pH, [OH^-], and pOH for this solution and identify the solution as acidic, basic, or neutral. (Solution shown in Appendix A.1.)

Strong Bases. Each of the strong bases are strong electrolytes (100% dissociating ionic salts), which are composed of the hydroxide (OH^-) ion in combination with monatomic cations of alkali or alkaline earth metals. When these electrolytes are placed in aqueous solution, they completely dissociate (Eq. (7)). The result is hydroxide ions and their countercations in amounts that are stoichio- metrically equivalent to the amount of strong base placed in solution. The reader should note that the dissociation reactions of strong acids and bases, illustrated in Eqs (6) and (7), are complete and essentially irreversible, and are denoted using one-way arrows.

NaOH(aq) → Na⁺(aq) + OH^-(aq) (7)

It should be further noted that the pH of highly concentrated strong acids and bases will deviate from that described here as at high concentrations, the pH is no longer equal to p^cH. This deviation of pH from pcH will also take place at high ionic strength, which takes place at higher (>0.1M) concentrations of electrolytes. At high ionic strength, an electrolyte solution no longer behaves as described in Eq. (7) because the increased proximity of oppositely charged ions allows significant electrostatic attraction to take place. Examples chosen for this work will be such that this deviation will not be significant.

Sample calculation: (b) Calculate pH and pOH in a 5.5 X 10^-3 M solution of Ba(OH)₂. (Solution presented in Appendix A.1.1.).