Volumetric Acid-Base Analyses

Acid-base neutralization reactions can be the basis of “volumetric" analyses (also called titrations) that provide the means of determining the molar amounts of unknown solutions of acids or bases. The process of a volumetric analytical method involves the addition, with precise volumetric control, of a solution containing a base or acid to a solution that contains an acid or base, respectively. The typical apparatus with which classical acid-base volumetric analyses are performed is shown in Figure 8.

Figure 8. Physical apparatus for classical volumetric analysis

The solution contained in the Erlenmeyer flask, which often contains the unknown solution being analyzed, is generally referred to as the “titrand" solution, whereas the solution in the buret, which is added to and is used to analyze the titrand solution, is referred to as the “titrant" solution. A titration method must permit the relatively accurate estimation of the location of a point in the reaction called the equivalence point.

As the titration is set up, an aliquot of the titrand solution is measured into an Erlenmeyer flask using a volumetric pipet usually in 25.00 or 50.00 mL volumes. In classical titration methods, the analyst estimates the location of the equivalence point with the help of a small amount of a strongly visibly colored substance known as an indicator (Section 2.9.2).

The concept of the “equivalence point" is fundamentally based on the same concept as acid-base neutralizations. Such a point is said to exist (or to have been reached) when the quantity of the acidic or basic species in the initial titrand solution and the quantity of the titrant solution that has been added are stoichiomet-rically equal, leading to their exact mutual neutralization. The amount of acid or base in the unknown (titrand) that was under analysis is hence determined based on the known amount of acid or base in the titrant that was consumed to reach the equivalence point.

Sample calculation: What volume of 0.1033 mol L^-1 NaOH is needed to reach the equivalence point in the titration of 18.00 mL of 0.0962 mol L^-1 NaH₂PO₄? (Solution presented in Appendix A.4.)

In general terms, titrations can be thought of as a techniques whose purpose is to “count" ions or molecules. Titrations of all varieties are based on fast chemical reactions (here, acid-base neutralization reactions) that provide essentially quantitative conversion of reactants into products. The chemical reactions must include the molecule or ion of interest in the unknown (i.e. titrand solution) as one of the reactants. The other reactant used (the titrant) must be added quantitatively so that its consumption indicates, ultimately, the amount of the target ion or molecule in the sample.

Acid-base titrations use one of the three types of fast acid-base chemical reactions: a reaction between a strong acid and a strong base (SASB), a weak acid and a strong base (WASB), or a strong acid and a weak base (SAWB). All three of these reactions proceed essentially to completion (i.e. with relatively large equilibrium constants) and occur very quickly (with large kinetic rate constants).

During all acid-base titrimetric analyses, the H₃O+ concentration (and consequently pH) in the solution that is being titrated changes in a systematic manner. Such pH changes are fundamental to (i) the behavior of pH indicators and (ii) the method by which the analyst judges the location of the equivalence point, and thus determines the concentration (or number of moles) of the unknown acid or base in the titrand solution.

It is necessary for the student of chemistry (or the analyst who performs acid-base titrations) to understand the nature of the pH changes that occur in the titrand solution over the course of a titration. It is also important to understand the way that these pH changes can trigger changes in the coloration of an indicator present in the reaction solution (Section 2.9.2).

Figure 9 presents two titration curves, for hypothetical titrations of (a) a monoprotic strong acid (curve a) and (b) a monoprotic weak acid with a monoprotic strong base titrant. The following discussion will be directed toward helping the reader understand qualitatively the nature of pH changes that occur in the course of these acid-base titrations.

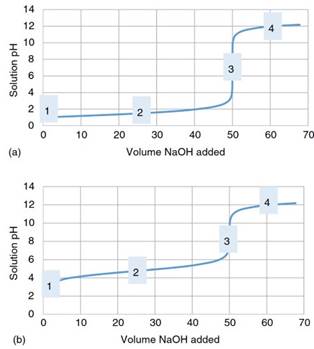
Figure 9. Titration (pH vs. volume of base added) curves for (a) the titration of a strong acid with a strong base and (b) titration of a weak acid with a strong base. Selected points (1-4) on the curves are indicated for reference and discussion

The titration curves for SASB and WASB titrations in Figure 9 were calculated based on model titrations of 50.00 mL, 0.100 M titrand solutions of HCl (curve a) or CH₃CO₂H (curve b) by the titrant 0.100M NaOH. The initial pH (i.e. Vb = 0.00 mL, point 1 in curves a and b) is determined by the activity of the acidic species initially present in the unknown (titrand) solution. Hence, in the SASB titration, the initial pH is simply determined by the initial concentration of H₃O+ ions that are present due to complete ionization of the strong acid (Section 2.4.1).

However, the calculation of the pH in the weak acid solution before any strong base has been added is essentially a calculation of the pH in a weak acid solution (Section 2.4.3). The reader might correspondingly note that the pH at point 1 in curve a is accordingly discernably lower than that for point 1 in curve b.

Next, we consider the point in the titration at which sufficient volumes of titrant has been added to consume one half of the quantities of acid that were initially present (i.e. point 2). This point in the progress of a titration is frequently referred to as the “half-equivalence’’ point. In the SASB titration, the pH at this point in the titration is simply controlled by the number of H₃O+ ions that remain in the solution after consumption of one half of the H₃O+ ions that were initially present in solution by their reaction with the OH^- ions from the strong base.

At the half-equivalence point for the WASB titration, the solution at point 2, which contains equal amounts of the protonated and deprotonated forms of the weak acid, essentially has the composition of a symmetrically buffered solution. The pH of the solution at this point in the titration curve is equal to the pK_a of the weak acid. Generally, when WASB titration curves are modeled, the pH of solutions over the entire region prior to the equivalence point (V_b < V_equiv) are determined using the Henderson-Hasselbalch equation (Eq. (24)).

At the equivalence point in the SASB titration, point 3, the autoionization of water is the only source of H₃O+ and OH^- ions, because (as discussed in Sections 2.8 and 2.9) the strong acid and strong base have completely neutralized each other leaving only spectator ions in solution. The autoionization of water is the only source of H₃O+ and OH^- ions in this solution, and thus the pH at the equivalence point in a SASB titration is 7.0. At the equivalence point in the W1ASB titration, also point 3, the weak acid has been quantitatively converted into the conjugate base form.

However, a secondary equilibrium which is based on the hydrolysis of the weak conjugate base, then controls the pH of the solution. Hydrolysis of the conjugate base, (Eq. (10), Section 2.4.4), creates a small but significant concentration of OH^- ions and shifts the pH upward from 7.0. Beyond the equivalence point, the solution pH in both the SASB and WASB titrations, point 4, is determined by the excess concentration of OH^- ions added from the strong base titrant.