Kinematics and Dynamics of the Valve Gear

For a good charge cycle, the valves must open and close quickly. However, the inertia of the valve gears needs to be taken into consideration in the design. Figure 10-22 shows the typical path of the cam stroke, cam speed x, and cam acceleration x over the angular displacement of the cam. These quantities correspond to the respective quantities of the valve movement.

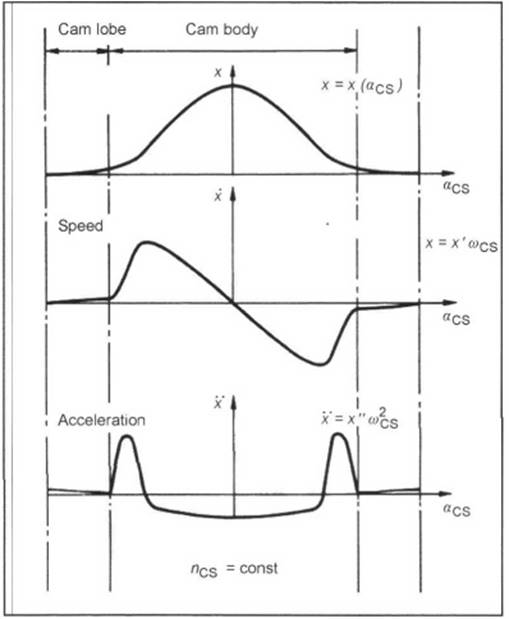
Fig. 10-22. Kinematics of the cams

The cam stroke or the cam contour is composed of the cam lobe and the cam body. At the cam lobe, the stroke speed x is slow so that common changes in the valve play do not generate strong impact pulses. The cam body determines the opening cross section for the charge cycle. The valve is closed by a deceleration corresponding to the cam lobe.

The stroke characteristic is a function of the camshaft angle α_NW. The following equation results for the stroke speed x:

In these equations, x' and x" are speed-independent functions that are determined only by the geometry of the cams. The cam shape also influences the characteristic of the valve movement. Figure 10-23 shows the relationship between stroke characteristic and cam shape in connection with a flat-based tappet. In the figure, the rotation of the cam has been replaced by the swing of the tappet in the opposite direction with a standing cam.

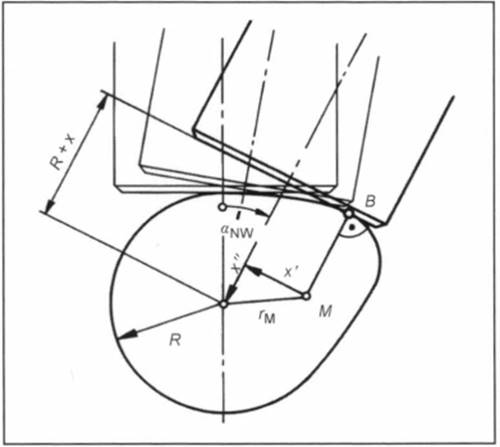
Fig. 10-23. Kinematics of the tappet stroke

The cam shape is the envelope curve of the tappet-sliding surface. For kinematic investigations, the cam drive can be replaced by thrust cranks whose articulation corresponds to the curvature midpoint M of the cam contour belonging to the contact point B. x' (rotated vector) and x" depend on the crank length (r_M) and position of the momentary thrust crank. We can see that the distance of the cam contact point B from the middle of the tappet is proportional to the speed. The tappet diameter must therefore be adapted to the maximum stroke speed.

It is important that friction is always present between the cam and tappet or rocker arm. In addition, there also must be friction between the valve and tappet or rocker arm for the valve to follow the cam stroke. The valve stroke may be recalculated corresponding to the valve rocker or valve lever ratio i — l₂/l₁. To test the grip, the force between the cam and tappet must be found. The inertia force and spring force must also be considered.

With a valve gear corresponding to Fig. 10-24, the following results for the force on the cam F_N:

If all the quantities on the cam side are "reduced," then the equation for the cam force is

This equation corresponds to the replacement system in Fig. 10-25. The following condition must be fulfilled for the grip:

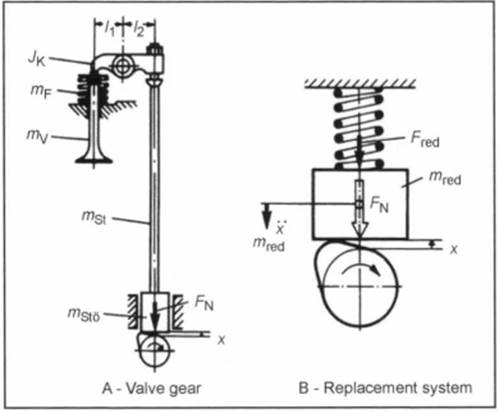
Fig. 10-24. Rigid valve gear

The characteristic of the tappet acceleration depends on whether or not the valve is lifted. Figure 10-25 shows the acceleration of the cam stroke x over the angular displacement of the cam at two camshaft speeds n_NW1 and n_NW2. If the characteristic of x intersects the curve – F_red/m_red, the grip is interrupted. This can occur only in the deceleration period of the main cam. There always exists speed above which lifting occurs.

Fig. 10-25. Lifting conditions for a valve gear

The valve gear should be designed so that the valve is not lifted at maximum camshaft speed (= ½ crankshaft speed). This is attained when the moved mass (m_red) is small and the spring force is high.