The Physics of Freezing: Homogeneous and Heterogeneous Ice Nucleation

A droplet of purest water, not disturbed by any agitation, can supercool to around -40 °C before instant nucleation takes place (Lorv et al. 2014). In that case, the Brownian molecular movement of the water molecules is so slow that larger clusters of molecules form, which initiate solidification in a hexagonal crystal lattice. As the nucleation in this case originates from water itself, it is called homogeneous nucleation. The cooling energy expended to achieve crystallisation is released as the heat of crystallisation, which can be recorded on a thermogram as the freezing exotherm (Fig. 4.6).

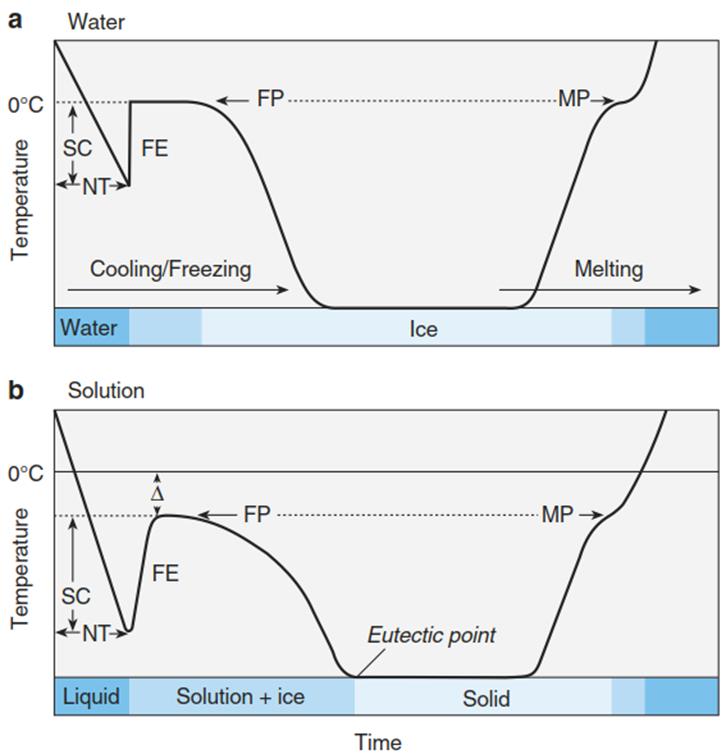
Fig. 4.6. Thermograms of the freezing and thawing processes of pure water a and of an aqueous solution of a low molecular weight compound b. Δ denotes freezing point depression. FE freezing exotherm, FP freezing point, MP melting point, NT nucleation temperature, SC supercooling

The melting process requires energy as well, referred to as the heat of fusion, and is recognised by a delay in warming during the thawing process (melting point (MP) in Fig. 4.6). When nucleation of crystallisation is initiated in other ways (e.g. by seeding with ice crystals), supercooling to a less negative temperature than for homogeneous nucleation is sufficient for crystallisation. This is called heterogeneous nucleation because elements of the environment trigger crystallisation.

These elements can be particular surface structures (e.g. of an ice crystal or a cell wall), whose microstructures can force the water clusters into a lattice-like structure which, together with the sub-zero temperature, facilitates crystallisation. Thus, heterogeneous nucleation requires less supercooling and, considering the situation in a plant tissue, with the physicochemical equilibrium between the extracellular ice and the cellular solutions, the proportion of water that crystallises is smaller and the freeze desiccation is less dramatic. This is important for preventing freezing damage by sudden ice formation.

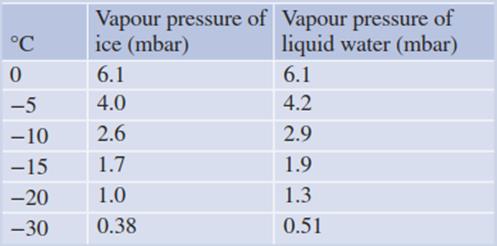
Table 4.2. Partial pressure of water vapour (in millibars) above ice and supercooled water

The water vapour pressure over ice is less than that over supercooled liquid water at the same sub-zero temperature (Table 4.2). In line with the lower water vapour pressure is the more negative water potential of ice compared with supercooled water. Both are directly dependent on the sub-zero temperature. The water potential of ice (ψ_ice) can be calculated from the vapour pressures over liquid water (Pwater) and over ice (Pice) by the following equation:

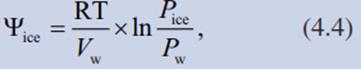
where V_w is the mole volume of water at the particular temperature. Therefore, at sub-zero temperatures, ice is thermodynamically more stable than supercooled water.

The water vapour pressure is also lower over aqueous solutions than over pure water and depends on the concentration of the solution— more precisely on the mole fraction (M) of water in the solution (Raoult’s law):

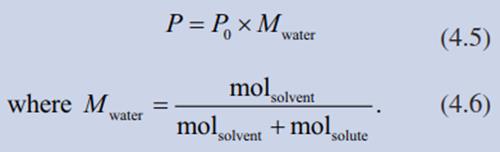
For dilute solutions it is the concentration of a solute(s):

where n = number of moles in a particular volume of water and the osmotic potential (water potential of the solution, π) is:

It follows that the freezing/melting point of a solution is lower than that of pure water (Fig. 4.6b) and that the depression (∆_Tm) is proportional to the concentration of the solution, whereby the molar ∆_Tm = 1.86 °C; thus the actual ∆_Tm = 1.86 x n_s (mole solute in 1 kg water (molality)).

This applies strictly to dilute (i.e. “ideal”) solutions. In concentrated solutions, interactions occur between the dissolved particles, resulting in an apparent reduction in the concentration. The factor a, by which the concentrations appears to decrease, is the activity factor.

The following considerations are important for the freeze dehydration of plant cells. Cooling of dilute solutions to sub-zero temperatures results first in freezing of pure water and an increase in the concentration of the cellular liquid. Separated by the cell wall, extracellular ice coexists with the liquid content of the cell, the proportions responding to the water potential of both compartments (within the cell, equilibrium of the water potentials of the organelles must also be assumed, otherwise considerable intracellular fluxes of water would occur between the organelles).