Non-evolutionary and Evolutionary Interpretations

Non-evolutionary 'theories' (actually, hypotheses). The non-evolutionary interpretations view senescence strictly in physiological, mechanistic terms of causality. It has been clearly established and known for decades that the rate of senescence has a genetic basis (Rose 1991; Ricklefs 2008). Undoubtedly, length of life in general is influenced by multiple genes whose effects on extending or shortening life influence numerous pathways and processes. Many of these mechanisms are conserved across phyla. The literature in this rapidly advancing frontier driven by research in medical gerontology is vast and details are beyond our scope here; some examples will be noted only in passing with commentary on similarities or differences, where known, among animals, plants, and microorganisms (for reviews see e.g., Finch 1990; Rose 1991; Kirkwood 2005; Ricklefs 2008; Roach and Carey 2014).

Research with animals including humans has demonstrated the effect on aging of singlegene mutations, many of which affect the insulin-like growth factor pathway, which is ubiquitous (Junnila et al. 2013). Growth hormone (somatotropin) and insulin-like growth factor (IGF-1) have multiple pleiotropic effects but the hormones act differently on glucose and lipid metabolism. Mutations affect longevity in mice; similar mutations have been observed in humans though their effect on longevity has not yet been ascertained. Considerable attention is focused on transcription factor p53 for its role as a tumor suppressor and as part of a generalized response to stress and cell death (Berkers et al. 2013; Salama 2014). Oxidative damage (Haigis and Yanker 2010; Selman et al. 2012) and injury associated with inflammatory responses (Ashley et al. 2012) have long been associated with cellular senescence.

An active area of biomedical research is directed at the role of telomeres and telomerase in cell biology and aging (Signer and Morrison 2013; Pfeiffer and Lingner 2013). Telomeres are nucleoprotein caps that protect the tips of chromosomes from end-to-end fusions, DNA degradation, and recombination. They contain short, noncoding sequences of DNA repeated for up to thousands of base pairs—for example, in humans the nucleotides 5'-TTAGGG-3' are reiterated about 10,000 times. Telomeric repeats are conserved across lineages as diverse as protists, mammals, plants, and fungi, and are probably common to all eukaryotes.

Cell division tends to shorten telomeres because RNA polymerase cannot fully replicate the lagging strand and DNA is lost at each replicative cycle. While the caps prevent coding sequences from attrition, eventually a critical threshold may be reached where DNA can no longer replicate. At this point chromosomes become physically and functionally aberrant, and the affected cells enter a ‘replicative cell senescence’ state or undergo programmed cell death. Thus the replicative life span of certain types of cells is finite, declines with age, and is regulated by telomeres together with the enzyme telomerase, which acts in part to synthesize telomeres. Telomerase enhances cellular replicative capacity and has been associated, as has telomere length or rate of erosion, with life span in various animal species (e.g., Heidinger et al. 2012; however see Monaghan and Haussmann 2006).

Interestingly, Skold et al. (2011) report that old (7-12 yr.), asexually reproducing strains of the colonial ascidian Diplosoma listerianum have lower telomerase activity and somewhat shorter telomeres and impaired asexual propagation rates compared with their recent, sexually produced progeny. So here is an example of a clonal, colonial, modular organism that may not have escaped senescence. The authors speculate that because these metazoans have evolved generally from sexual ancestors they may have retained the constraint of somatic senescence as an evolutionary legacy necessitating periodic sexual reproduction for rejuvenation.

In plants, the mechanistic basis of ‘senescence’ of cells and organs in the physiological context of normal cell differentiation and organogenesis is relatively well documented (Pedersen 1999; Nooden 2004; Thomas 2013). The process typically follows an orderly (coordinated) programmed cell death or apoptosis-like process under the control of hormones and frequently nutrient source-sink relationships and remobilization of nutrients (Schip- pers et al. 2015; Van Durme and Nowack 2016). For example, in tissues destined to be the water-conducting (vascular xylem) elements, precursor cells that are living and meristematic undergo complex ontogenetic changes to become elongate, interconnected, dead cells specialized for water transport.

Other examples of coordinated events include the staging of leaf and flower senescence and possibly even the rapid death (‘whole-plant senescence’) that follows immediately upon the flowering stage in monocarpic (semelparous) plants, mainly annuals and biennials. However, unlike the case in animals, these senescence events do not appear to result from the action of deleterious genes or somatic mutation. Such episodes of plant ‘senescence’ seem fundamentally distinct from the life history or evolutionary context of senescence of the animal individual, though some molecular causal mechanisms may be shared.

Telomere attrition and telomerase activity have received limited attention in plants; as a senescence mechanism they have not risen to the level of potential importance in plant senescence that they have in animals. This appears due in large part to the greater tolerance of telomeric damage in plants, perhaps attributable to developmental plasticity, including the organization of their various meristems (Riha et al. 2001; Thomas 2013; Amiard et al. 2014). Thus, where gradual, whole-plant senescence occurs among polycarpic plants, the causal mechanisms remain unclear and are usually attributed to multiple, fairly general problems related to accumulating live and dead biomass, size in the case of trees, transport, respiratory tissue burden, and increased susceptibility to herbivores and pathogens (Pedersen 1999).

To summarize, there is intense focus on mechanisms of cellular senescence in animal models and humans driven largely by research in medical geriatrics. In plants, senescence research has emphasized physiological mechanisms associated with nutrient remobilization and developmental staging of such relatively local events as leaf or flower senescence, rather than whole-plant senescence. The latter has been considered with respect to systemic senescence of annual plants, with Arabidopsis thaliana being a favorite model (e.g., Morales and Munne-Bosch 2015; Wuest et al. 2016).

In the case of both plants and animals, it is not clear whether cellular senescence is the cause or consequence of senescence at the organismal level or, more broadly speaking, how fruitful such reductionist approaches ultimately will be in explaining organismal senescence mechanistically. Similarly, it is not clear whether results from research models can be extrapolated to other organisms.

Evolutionary 'theories' (hypotheses). The classic so-called theories reviewed briefly below were developed largely with humans and other animals in mind. They attempt to explain the paradox of why selection has not removed a conspicuously disadvantageous trait lowering organism fitness. Seminal early work on the evolutionary biology of senescence argues that the phenomenon reflects the unavoidable consequence of the timing of gene action and declining force of natural selection (Medawar 1946, 1952; Williams 1957; Hamilton 1966; Kirkwood and Holliday 1979). Stearns (2000, p. 482) summarizes the evolutionary interpretations as consolidating to senescence being “... a byproduct of selection for reproductive performance”.

Fisher's seminal observation. The early studies built upon the now famous insights on population increase and reproductive value by Fisher (1930, pp. 27-30), whose aim was to understand how rates of death and reproduction of a population of organisms aligned with the force of natural selection. With respect to persons of any age he asked specifically (p. 27) ... “what is the present value of their future offspring? ... To what extent will persons of this age, on the average, contribute to the ancestry of future generations? ... the direct action of Natural Selection must be proportional to this contribution.” For humans, reproductive value rises with age to puberty and then declines to a minimum beginning in about mid-life. Fisher went on to note (p. 29), prophetically but seemingly in passing, that the mortality rate in humans was generally the inverse of the plot of reproductive value, .. points which qualitatively we should anticipate[,] if the incidence of natural death had been to a large extent moulded [sic] by the effects of differential survival” (Fig. 6.9).

Thus, reproductive value is the product of the probability of survival to a particular age and the rate of production of offspring (fecundity) (for synopsis see Begon et al. 1996; pp. 530-532). If we ignore for a moment the numbers of offspring and look at just the likelihood that an organism such as a human will reproduce at any given age, the probability distribution rises sharply from zero prior to sexual maturity to a peak followed by steep decline as potentially reproductive individuals are removed by death from the population, as Fisher had noted. If we consider next the fecundity component of reproductive value, this will decline with adult age largely if not entirely because of senescent changes.

So it cannot be invoked without circular reasoning to explain why the phenomenon occurs. The key, however, is that over time, even without senescence, there will be a cumulative probability of death simply from random events. This dictates the decline in reproductive probability illustrated because the likelihood of reproducing at an age clearly depends on the chances of surviving to that age (Fig. 6.9).

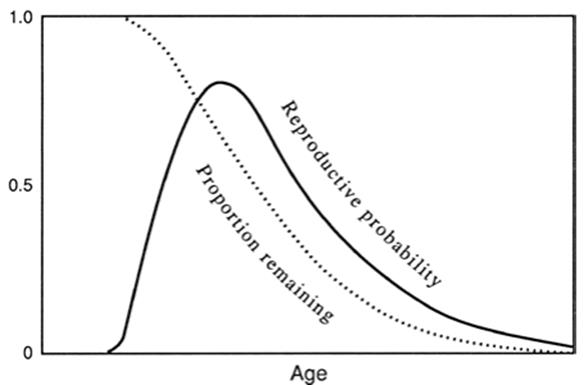
Fig. 6.9. Relationship between age and probability of reproduction (for some organisms—see text; theory and graph based on Williams 1957). The solid line is the reproductive probability distribution curve, which measures the expectation that the organism will reproduce at any given age. Area under this curve thus reflects the total expectation for reproduction. The dotted curve is the proportion of the total probability for reproduction remaining at any given age. It is also a measure of natural selection in force at any age for such organisms because selection acts through reproduction and will be highest when the potential for reproduction is highest. The graph is similar but not identical to Fisher's (1930) concept of reproductive value (see text), and to a plot of rate of reproduction versus age as described by Kirkwood and Holliday (1979). Plot redrawn from Williams (1957); reproduced from Evolution by permission of The Society for the Study of Evolution and Allen Press, Lawrence, Kansas ©1957

Medawar's insight. By such reasoning, it fell to Medawar to avoid the pitfall that caught his predecessors. His early ideas (1946), influenced by Fisher’s reasoning, were presented in a lecture at University College, London, in 1951, and published as an essay shortly thereafter (1952). He circumvented the tautology by not first assuming that senescence was due to wear and tear and then explaining it in those terms, but rather asked why older organisms should be decrepit and worn out. His reasoning used the analogy of a population of 1000 ‘potentially immortal’ glass test tubes and followed their fate over time.

The population declined progressively due (only) to random breakage, i.e., it did not become increasingly prone to ‘death’ (in other words, Medawar initially ignored any inherent imperfections in the glass, i.e., he took as a premise that it did not intrinsically ‘senesce’). The attrition rate therefore was exponential, the chances of dying did not change with time; for illustration he used a random attenuation rate of 10% or 100 tubes per month. The broken tubes were replaced with 100 new ones each month so the population size remained constant, and after a number of years of losses and replacements the age distribution stabilized (Fig. 6.10). Thus, regardless of age, the probability of survival for any tube from one month to the next is the same (0.9) and for any month (x) in question can be given as 0.9^x. Obviously, the older the tubes are, the fewer there will be in that age group simply because they will have been exposed longer to random breakage.

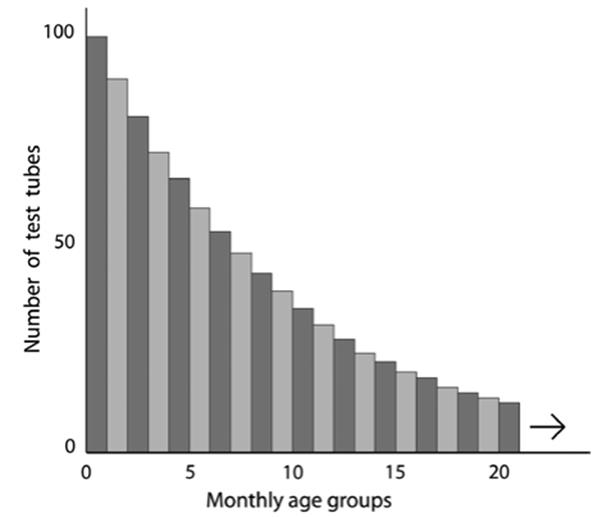
Fig. 6.10. Stable age distribution after many months in a population of 1,000 test tubes ‘dying’ randomly at a constant rate of accidental breakage and replacement of 10% per month. Thus, in month class 0–1 there are 100 tubes; then 90 aged 1–2 months; et seq. This pattern gave rise to the terminology ‘potentially immortal’ in the senescence and longevity literature to describe organisms where the chances of dying do not change with time. Such descriptors date back to the work of Medawar (1952) and extend to this day. Note that if the tubes are allowed to ‘reproduce themselves’ at some constant rate per tube regardless of age, the younger age classes will nevertheless contribute more offspring to the population purely because there are more such tubes than in the older classes. Plot and theory based on Medawar’s lecture delivered in 1951, published in 1952 for University College, London by H.K. Lewis & Co., 1952

In the next step, Medawar allowed the test tubes to maintain their own numbers rather than being replaced by the investigator or, in Medawar’s words, to reproduce themselves (‘no matter how’ pp. 16-17) at an average rate of 10% per month, with each remaining tube contributing an equal share. This means that in aggregate 100 tubes would be added each month and since there are 900 remaining, each tube, regardless of age, contributes 1/9 of a tube to the population monthly.

This is the same as saying that fecundity on a per capita basis is not changing with age. The key insight here is that although the average death rate and birth rate per tube does not change among the age classes, the contribution to the population of the older classes does decline, not because the tubes are more fragile but because there are fewer of them. This is comparable to saying that the older the age group the lower its overall reproductive value.

As a final step, Medawar imposed mortality on the tubes by allowing some to disintegrate spontaneously and asked what the effect the timing of such lethal ‘genetic’ events would be on the population. Clearly the earlier such a disaster occurs, the greater is its impact on the population: at the advanced age of 5 years it would be virtually negligible because only a tiny fraction of that age group (probability of survival to that age =0.0018 or <1 in 500 total population) would be still ‘alive’.

At 12 months (an age reached by about 28% of the test tubes), the destruction would be severe but not disastrous because that group would have previously contributed most of its offspring to the population. Medawar’s important conclusion (1952, p. 18) was “... that the force of natural selection weakens with increasing age—even in a theoretically immortal population, provided only that it is exposed to real hazards of mortality” and further (p. 19) "... the selective advantage or disadvantage of a hereditary factor is rather exactly weighted by the age in life at which it first becomes eligible for selection. A relatively small advantage conferred early in life of an individual may outweigh a catastrophic disadvantage withheld until later".

Expansion by Williams, Hamilton, and others. If the potency of natural selection is maximal near the age of puberty and begins to decline subsequently in populations such as humans, a key implication of Medawar’s analogy is that the timing in expression of genes with a beneficial effect will tend to move forward to youth whereas those with deleterious effect will move backward to older age. Those genes will remain in the gene pool, however, because selection at that point is insufficient to remove them and they will tend to accumulate in the population (the special case of antagonistic pleiotropy is discussed later; Williams 1957).

Candidate late-manifesting human genes include those involved in Huntington’s chorea, neurodegenerative diseases, immunological dysfunction, cancers, cardiovascular problems, stroke, etc., that in aggregate are associated with the characteristic physiological decline and dysfunction of older age. It bears repeating that Medawar’s insight was that such a sequence of events could arise even in his ‘theoretically immortal’ non-senescent population subject only to the hazards of extrinsic accident.

Although Medawar alluded to the possibility of pleiotropy and linkage in discussing the implications of his scheme (1952, see p. 19), he had in mind mutation accumulation and it remained for Williams (1957) to take up pleiotropy at length. Williams emphasized the role of genes with pleiotropic effects at different stages of life, drawing on Medawar’s work to show that those with beneficial early effects would tend to spread in a population even if causing comparable reduced survival later (the ‘antagonistic pleiotropy’ model). Williams emphasized the importance of the separation of germ line and soma, arguing that senescence is an evolved characteristic of the soma. Thus, absence of a clear soma meant absence of senescence. Returning to our earlier examples, organisms reproducing by fission such as bacteria, many protozoa and yeasts, and a few animals, lack a clear age structure and soma; theoretically they should not senesce. Importantly, and particularly in the context of confusion between individual (ramet) senescence and clonal senescence in the ensuing literature, Williams observed (p. 403) that “while asexual clones should not show senescence, asexually reproducing individuals may be regarded as having somas and they should, according to the theory, show senescence” [emphasis added]. It is worth noting in passing that the whole-plant senescence typified by monocarpic plants contradicts one of Williams’ (1957) key postulates that senescence should be found only in organisms with a distinct germ line and soma. Plants do not segregate such tissues until immediately before flowering yet some clearly senesce.

In overview, Williams broadly viewed the evolution of senescence as a result of two opposing forces: one, an indirect force tending to increase the rate of senescence as an adverse side effect of early-acting, otherwise favorable genes, the cost of which is later decline (senescence); the other, a direct force tending to reduce the price by slowing the rate of senescence. The balance between these forces would determine the pattern exhibited by any particular species. Any factor in the life history decreasing the rate of decline in reproductive probability distribution (survival and fecundity) would increase selection against senescence. Subsequently, Charlesworth (1980, pp. 206-209; 1994, pp. 198-200) described Williams’ idea in population genetics terms.

Rather than adopting Fisher’s (1930) somewhat nebulous (‘indirectly relevant’ according to Hamilton 1966) concept of reproductive value in interpreting the force of natural selection as Medawar and Williams had accepted intuitively, Hamilton used a different criterion in his tightly argued mathematical analysis. This influential paper became a benchmark in the assessment of senescence. He advocated that the Malthusian parameter (equivalent to r) be used to assess age-specific survival and fecundity and noted that the change in reproductive value over time differed from the sensitivity of fitness to changes in survival and fecundity. Among other things, this led to different predictions with respect to the timing of gene action and onset of senescence in some situations (pp. 21-25 in Hamilton and pp. 190198 in Charlesworth 1994; Charlesworth 2000).

Indeed, in cases where fecundity increases exponentially with adult age (as is the case for many trees), reproductive value as a gauge of selection intensity does so as well and predicts the reverse of senescence (see Baudisch, below). Reproductive value depends on the individual having survived to a given age x discounting population growth to that age, whereas Hamilton’s measure of r is an assessment of the fitness effect of change in death at age x for individuals at the time of conception (Chap. 5 in Charlesworth 1994; see also Chap. 1 in Rose 1991 and Charlesworth 2000).

Reproductive value generally reaches its maximum shortly after the age of first reproduction, whereas Hamilton’s measures of the sensitivity of fitness to changes in survival and fecundity decline throughout reproduction. Hamilton therefore emphasized and Charlesworth later clarified the importance in Hamilton’s calculations of early reproduction, and accordingly the role of mutations increasing early survival compared to those acting later. This effect would lead to life histories with lower age-specific mortality early in adulthood and higher mortality rates later.

Hamilton took as the limiting case for potential senescence a hypothetical organism like Volvox (described in Chap. 4) in which all cells divided synchronously and fertility increased exponentially with age indefinitely. At the tetrad stage one cell is ejected to become a spore and the other three separate, position themselves in the enlarging sphere, and continue growing in geometric progression at the ratio of three per every two cell generations. No limits to growth are imposed in this extreme case so growth, expansion, fertility, continue exponentially ... “so that all its members are immortal” (p. 25). Yet even Hamilton’s ‘Utopian population’ is not immune from the workings of natural selection and genetic variation. He accepts Williams’ (1957) idea of antagonistic pleiotropy as well as noting that a mortality factor imposed early, however small, shows that selection acts to resist it at the cost of increased vulnerability later. Thus, Hamilton’s prophetic words have echoed down through the decades: “senescence will tend to creep in” (p. 25); and (p. 26) ... “for organisms that reproduce repeatedly, senescence is to be expected as an inevitable consequence of the working of natural selection”.

Baudisch (2005, 2008; Vaupel et al. 2004), however, argues that Hamilton’s conclusions are a result of his restrictive modeling assumptions and parameterization. Different assumptions and parameters lead to different conclusions, even within Hamilton’s original model (Bau- disch 2005). Instead of emphasizing the impact of mutation accumulation on age-specific fitness, she and colleagues have focused on optimization of trade-offs in shaping mortality and fertility schedules, arguing that the force of natural selection actually can increase with age in some organisms such as plants as alluded to earlier. Caswell and Salguero-Gomez (2013) use different terminology but reach similar conclusions in a model that considers plants both in terms of age and stage of development.

Kirkwood and colleagues (e.g., Kirkwood 1977; Kirkwood and Holliday 1979, 1986; Kirkwood and Rose 1991; Abrams and Ludwig 1995) explained senescence in terms of physiological ecology, specifically pertaining to optimal resource allocation (e.g., see Chap. 3 and Partridge and Barton 1993). Kirkwood asked how the life history of an organism should be shaped by allocating resources and energy optimally between somatic upkeep and reproductive function. Obviously the production of progeny requires some somatic investment, but how much?

They viewed maintenance costs as accrued from: (i) construction of nonrenewing parts such as teeth; (ii) cell renewal, such as those of the skin and immune system; and (iii) intracellular upkeep and traffic. The soma is merely a means of transmitting genes to one’s progeny. A close to error-free (non-senescent) soma would necessitate a very high level of maintenance at the expense of input to progeny; conversely, too little invested in a soma could result in no or negligible reproduction. In their model, the investment that maximizes fitness (rate of increase, r) for an iteroparous species is a strategy that allows some unrepaired somatic defects (senescence). This ‘disposable soma’ theory is actually a variant of Williams’ model, a potential explanation for one way it might operate. Even in the absence of a soma, a single-celled organism like a bacterium faces trade-offs between maintenance (survival) functions and reproduction (Nystrom 2002).

In overview, it appears that where organismal senescence occurs in various phyla it can reflect the declining force of natural selection with age. Theoretical models support such an interpretation, and the limited experiments to date on model organisms such as Drosophila that vary the force of natural selection at different ages, support the evolutionary interpretation of aging. The underlying mechanisms remain unclear and may include the accumulation of deleterious genes, the pleiotropic impact of the timing in gene action, soma/gene tradeoffs, or other factors as yet unidentified.