Medical Image Segmentation

A fundamental operation in medical image analysis is the segmentation of anatomical structures. It is not surprising that segmentation of medical images has been an important research topic for a long time. It essentially involves partitioning an image into distinct regions by grouping together neighboring pixels that are related.

The extraction or segmentation of structures from medical images and reconstructing a compact geometric representation of these structures is fairly complex because of the complexity and variability of the anatomical shapes of interest. Inherent shortcomings of the acquired medical images, such as sampling artifacts, spatial aliasing, partial volume effects, noise, and motion, may cause the boundaries of structures to be not clearly distinct.

Furthermore, each imaging modality with its own characteristics could produce images that are quite different when imaging the same structures. Thus, it is challenging to accurately extract the boundaries of the same anatomical structures. Traditional image processing methods are not easily applied for analyzing medical images unless supplemented with considerable amounts of expert intervention.

There has been a significant body of work on algorithms for the segmentation of anatomical structures and other regions of interest that aims to assist and automate specific radiologic tasks. They vary depending on the specific application, imaging modality, and other factors. Currently, no segmentation method yields acceptable results for different types of medical images.

Although general methods can be applied to a variety of data, they are specific for particular applications and can often achieve better performance by taking into account the specific nature of the image modalities. In the following subsections, the most commonly used segmentation methods are briefly introduced.

Thresholding. Thresholding is a very simple approach for segmentation that attempts to partition images by grouping pixels that have similar intensities or range of intensities into one class and the remaining pixels into another class. It is often effective for segmenting images with structures that have contrasting intensities.

A simple approach for thresholding involves analyzing the histogram and setting the threshold value to a point between two major peaks in the distribution of the histogram. Although there are automated methods for segmentation, thresholding is usually performed interactively based on visual assessment of the resulting segmentation (20). Figure 8 shows the result of a thresholding operation on an MR image of brain where only pixels within a certain range of intensities are displayed.

The main limitations of thresholding are that only two classes are generated, and that it typically does not take into account the spatial characteristics of an image, which causes it to be sensitive to noise and intensity inhomogeneities which tend to occur in many medical imaging modalities. Nevertheless, thresholding is often used as an initial step in a sequence of image-processing operations.

Region-Based Segmentation. Region growing algorithms have proven to be an effective approach for image segmentation. The basic approach in these algorithms is to start from a seed point or region that is considered to be inside the object to be segmented. Neighboring pixels with similar properties are evaluated to determine whether they should also be considered as being part of the object, and those pixels that should be are added to the region.

The process continues as long as new pixels are added to the region. Region growing algorithms differ in that they use different criteria to decide whether a pixel should be included in the region, the strategy used to select neighboring pixels to evaluate, and the stopping criteria that stop the growing. Figure 9 illustrates several examples of region growing-based segmentation.

Figure 9. Segmentation results of region growing with various seed points obtained by using Insight Toolkit

Like thresholding-based segmentation, region growing is seldom used alone but usually as part of set of image-processing operations, particularly for segmenting small and simple structures such as tumors and lesions. Disadvantages of region growing methods include the need for manual intervention to specify the initial seed point and its sensitivity to noise, which causes extracted regions to have holes or to even become disconnected.

Region splitting and merging algorithms evaluate the homogeneity of a region based on different criteria such as the mean, variance, and so on. If a region of interest is found to be inhomogeneous according to some similarity constraint, it is split into two or more regions. Since some neighboring regions may have identical or similar properties after splitting, a merging operation is incorporated that compares neighboring regions and merges them if necessary.

Segmentation Through Clustering. Segmentation of images can be achieved through clustering pixel data values or feature vectors whose elements consist of the parameters to be segmented. Examples of multidimensional feature vectors include the red, green, and blue (RGB) components of each image pixel and different attenuation values for the same pixel in dual-energy x-ray images. Such datasets are very useful as each dimension of data allows for different distinctions to be made about each pixel in the image.

In clustering, the objective is to group similar feature vectors that are close together in the feature space into a single cluster, whereas others are placed in different clusters. Clustering is thus a form of classification. Sonka and Fitzpatrick provide a thorough review of classification methods, many of which have been applied in object recognition, registration, segmentation, and feature extraction. Classification algorithms are usually categorized as unsupervised and supervised.

In supervised methods, sample feature vectors exist for each class (i.e., a priori knowledge) and the classifier merely decides on how to classify new data based on these samples. In unsupervised methods, there is no a priori knowledge and the algorithms, which are based on clustering analysis, examine the data to determine natural groupings or classes.

Unsupervised Clustering.Unlike supervised classification, very few inputs are needed for unsupervised classification as the data are clustered into groupings without any user-defined training. In most approaches, an initial set of grouping or classes is defined. However, the initial set could be inaccurate and possibly split along two or more actual classes. Thus, additional processing is required to correctly label these classes.

The k-means clustering algorithm(28,29) partitions the data into k clusters by optimizing an objective function of feature vectors of clusters in terms of similarity and distance measures. The objective function used is usually the sum of squared error based on the Euclidean distance measure. In general, an initial set of k clusters at arbitrary centroids is first created by the k-means algorithm.

The centroids are then modified using the objective function resulting in new clusters. The k-means clustering algorithms have been applied in medical imaging for segmentation/classification problems. However, their performance is limited when compared with that achieved using more advanced methods.

While the k-means clustering algorithm uses fixed values that relate a data point to a cluster, the fuzzy k- means clustering algorithm (also known as the fuzzy c- means) uses a membership value that can be updated based on distribution of the data. Essentially, the fuzzy k-means method enables any data sample to belong to any cluster with different degrees of membership. Fuzzy partitioning is carried out through an iterative optimization of the objective function, which is also a sum of squared error based on the Euclidean distance measure factored by the degree of membership with a cluster.

Fuzzy k-means algorithms have been applied successfully in medical image analysis, most commonly for segmentation of MRI images of the brain. Pham and Prince were the first to use adaptive fuzzy k-means in medical imaging. In Ref. 34, Boudraa et al. segment multiple sclerosis lesions, whereas the algorithm of Ahmed et al. uses a modified objective function of the standard fuzzy k-means algorithm to compensate for inhomogeneities. Current fuzzy k-means methods use adaptive schemes that iteratively vary the number of clusters as the data are processed.

Supervised Clustering.Supervised methods use sample feature vectors (known as training data) whose classes are known. New feature vectors are classified into one of the known classes on the basis of how similar they are to the known sample vectors. Supervised methods assume that classes in multidimensional feature spaces can be described by multivariate probability density functions.

The probability or likelihood of a data point belonging to a class is related to the distance from the class center in the feature space. Bayesian classifiers adopt such probabilistic approaches and have been applied to medical images usually as part of more elaborate approaches. The accuracy of such methods depends very much on having good estimates for the mean (center) and covariance matrix of each class, which in turn requires large training datasets.

When the training data are limited, it would be better to use minimum distance or nearest neighbor classifiers that merely assign unknown data to the class of the sample vector that is closest in the feature space, which is measured usually in terms of the Euclidean distance. In the k- nearest neighbor method, the class of the unknown data is the class of majority of the k-nearest neighbors of the unknown data.

Another similar approach is called the Parzen windows classifier, which labels the class of the unknown data as that of the class of the majority of samples in a volume centered about the unknown data that have the same class. The nearest neighbor and Parzen windows methods may seem easier to implement because they do not require a priori knowledge, but their performance is strongly dependent on the number of data samples available. These supervised classification approaches have been used in various medical imaging applications.

Model Fitting Approaches. Model fitting is a segmentation method where attempts are made to fit simple geometric shapes to the locations of extracted features in an image. The techniques and models used are usually specific to the structures that need to be segmented to ensure good results. Prior knowledge about the anatomical structure to be segmented enables the construction of shape models. In Ref. 42, active shape models are constructed from a set of training images.

These models can be fitted to an image by adjusting some parameters and can also be supplemented with textural information. Active shape models have been widely used for medical image segmentation.

Deformable Models. Segmentation techniques that combine deformable models with local edge extraction have achieved considerable success in medical image segmentation. Deformable models are capable of accommodating the often significant variability of biological structures. Furthermore, different regularizers can be easily incorporated into deformable models to get better segmentation results for specific types of images. In comparison with other segmentation methods, deformable models can be considered as “high-level segmentation’’ methods.

Deformable models are referred by different names in the literature. In 2-D segmentation, deformable models are usually referred to as snakes, active contours, balloons, and deformable contours. They are usually referred to as active surfaces and deformable surfaces in 3-D segmentation.

Deformable models were first introduced into computer vision by Kass et al. as ‘‘snakes’’ or active contours, and they are now well known as parametric deformable models because of their explicit representation as parameterized contours in a Lagrangian framework. By designing a global shape model, boundary gaps are easily bridged, and overall consistency is more likely to be achieved.

Parametric deformable models are commonly used when some prior information of the geometrical shape is available, which can be encoded using, preferably, a small number of parameters. They have been used extensively, but their main drawback is the inability to adapt to topology. Geometric deformable models are represented implicitly as a level set of higher dimensional, scalar-level set functions, and they evolve in an Eulerian fashion.

Geometric deformable models were introduced more recently by Caselles et al. and by Malladi et al.. A major advantage of these models over parametric deformable models is topological flexibility because of their implicit representation.

During the past decade, tremendous efforts have been made on various medical image segmentation applications based on level set methods. Many new algorithms have been reported to improve the precision and robustness of level set methods. For example, Chan and Vese proposed an active contour model that can detect objects whose boundaries are not necessarily defined by gray-level gradients.

When applying for segmentation, an initialization of the deformable model is needed. It can be manually selected or generated by using other low-level methods such as thresholding or region growing. An energy functional is designed so that the model lies on the object boundary when it is minimized.

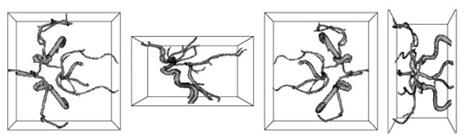
Figure 10. Different views of the MRA segmentation results using the capillary active contour

Yan and Kassim proposed the capillary active contour for magnetic resonance angiography (MRA) image segmentation. Inspired by capillary action, a novel energy functional is formulated, which is minimized when the active contour snaps to the boundary of blood vessels. Figure 10 shows the segmentation results of MRA using a special geometric deformable model, the capillary active contour.