Drivers of Water Flow Between the Soil and the Atmosphere

In soils and in plants, water is not freely available but is bound mainly to molecules or surfaces. In soil science and ecology, the following distinctions are made:

- Constituent water comprises water that has been used in the plant metabolism.

- Hydration water describes the layer of water molecules that is arranged as dipoles around ions. The strength of the binding increases with the charge of the hydrated ion and decreases with its radius. Thus, Na⁺ has a larger hydration layer than K⁺ (Luttge and Higinbotham 1979). All polar groups of organic molecules have a hydration layer. Of the total water in a leaf, 5-10% is therefore not freely available.

- Capillary water in cell walls and in the fine pores of soils is subject to capillary forces. The rise of the water column in a capillary (h, measured in metres) is, as a first approximation, inversely proportional to the radius (r) of the capillary, because the water mass and the gravitational force affecting it (πr²hpg) must be balanced against the cohesive force produced by the surface tension (2πrσ_w cosα). Neglecting the contact angle, α (cosα = 1) for a 0° angle, the following equation applies (Nobel 2009):

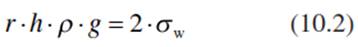
where h is the height in metres to which the water column rises, p is the density of water (998 kg m^-3 at 20 °C), g is the acceleration of the Earth (9.8 m s^-2), r is the radius of the capillary (metres) and σ_w is the surface tension of water (0.0728 N m^-1 at 20 °C). Thus, the pressure (P) in a capillary, the so-called capillary force (as measured in Newtons) is:

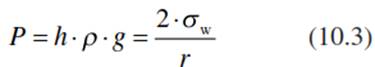
and the height of the meniscus is calculated as:

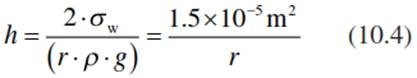
In a clean (lipid-free) glass capillary 3 pm in diameter (with a 1.5 pm radius), water rises 10 m. In a xylem vessel of 30 μm (typical for tracheids of conifers), water rises by capillary forces only 1 m, and in the 300 μm trachea of deciduous trees the water rises only 0.1 m via capillarity. Thus, the capillary force is not sufficient to lift water into the canopy of trees and therefore does not provide the lifting power required for the flow of water.

Cell water is osmotically bound (e.g. in the plant vacuole). The osmotic pressure, П, depends on the number of particles per mole (n), the concentration (c_n), the gas constant, R (8.3144 Pa m^-3 mol^-1 K^-1) and the temperature, T (in Kelvins):

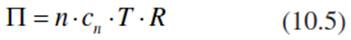
In contrast to Chap. 6, the osmotic pressure is expressed here as positive pressure measured in Megapascals. This concept is based on an experiment that also demonstrates the phenomenon of osmosis: A closed chamber, called an osmometer (Pfeffer 1877), is divided by a semiperme- able membrane into two compartments. The membrane allows passage of water molecules but is impermeable for ions. One compartment of the chamber is filled with distilled water, the other with a salt solution. In this case, free water is able to flow into the chamber with the salt solution, building up hydrostatic pressure. The level of water rises in the salty compartment, compared with the chamber containing free water, until the water column balances gravity. The height of the water column corresponds to the osmotic pressure. It is 2.48 MPa for a 1 molar solution.

To describe the flow of water between the very heterogeneous compartments of the plant and the environment, it is necessary to quantify the availability of water uniformly. This is possible by the definition of a common force for water transport, the water potential:

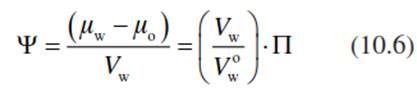
where μ_w is the chemical potential in the system (J mol^-1) and μ_o the chemical potential of a reference system—that is, of pure liquid water at a given temperature and at normal pressure (atmospheric pressure). Dividing the difference of the chemical potentials (μ_w - μ_o) by the molar volume of liquid water (V_w) results in the water potential being defined in units of pressure (in Pascals) (Slatyer 1967; Walter and Kreeb 1970). Thus, the water potential describes the driving force for water movement in units that can be measured easily. V_w is slightly dependent on temperature and atmospheric pressure. V_W^o expresses the molar volume of pure water (П = 0) in physical normal conditions.

In the gaseous phase the water potential is proportional to the relative humidity (Nobel 2009):

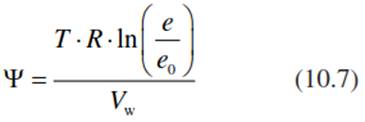
where e/e₀ expresses the vapour pressure of bound water (e.g. in solution or solid material) relative to that of free water. e/e₀ corresponds to the relative humidity. The proportion e/e₀ is also called water activity—describing, for example, the degree of swelling of colloids—and thus characterises the conditions for life of microorganisms or poikilohydric plants (Walter and Kreeb 1970).

As the chemical potential of bound water, μ_w, is more negative than that of free water, μ_o (energy has to be added to change, for example, bound water in a salt solution into the state of free water), the water potential has a negative sign. Water movement occurs from sites with high (more positive) potential to sites with low (more negative) potential. Thus, the water potential describes the state of water of the atmosphere, soils, plants or particles, and the water potential difference between compartments is the driving force for water flow.

Using the water potential, it is possible to describe water status and water flows in singlephase systems (e.g. in a plant), as well as in phase transitions (e.g. water uptake from soils; Chap. 6). In a cell with good water supply and without any water flow, the osmotic pressure is compensated by the counter-pressure of the cell wall—the turgor pressure (P_c)—which can be measured as a positive pressure in a cell (except for xylem cells where it is negative because of their special structure). With freely available water, the water potential of the cell or tissue is zero. With decreasing water content of the cell, the turgor pressure decreases and the osmotic pressure increases because of the increasing concentration of the residual solution in the cell. The difference, P - П, corresponds to the water potential, ψ, which becomes increasingly more negative when the cell dries out. In a tissue under such conditions, water flows, for example, from the cell wall into this cell until the water potential gradient equilibrates. If desiccation of the cell continues, the water potential may become equal to the osmotic pressure (П = -ψ). At this point of turgor loss, plants start to wilt and cells start plasmolysis.

The water potential of the living cell is described as:

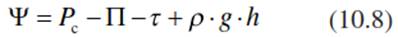
where τ represents an additional force describing the binding of water in the membrane-free matrix of the cell wall and their coating with water molecules (the so-called matrix potential; Sect. 10.2.1), which depends on surface forces and not on the number of particles in the solution, as in the case of П. This is important under saline conditions (Kramer and Boyer 1995). p g h is the water pressure, with p describing the density of water, g the gravitational force (9.807 m s^-2 at 45° latitude) and h the height of the meniscus above-ground (in metres; see Eq. 10.3). Thus, the water potential is dependent on the turgor pressure, the osmotic pressure, the chemical binding of water, surface properties and gravity, which is particularly important for tall trees Eq. 10.8, where the water potential is different in the root and shoot, depending on the height. Many authors also use the expression:

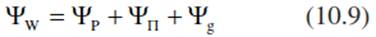
where ψ_W is the water potential in the cell, ψ_P is the turgor, ψ_П is the osmotic potential and ψ_g is the potential due to gravity.

If the water potential between the plant, soil and air is balanced, there is no net transpiration flux. In nature, this may occur at night or during early morning at high air humidity. Therefore, the early morning predawn water potential (ψ_predawn) in a plant is used to characterise the water conditions of the soil in the zone from which the roots obtain their water, which is in equilibrium with the leaf under conditions of no transpiration. With transpiration, a gradient in water potentials develops between the soil and the atmosphere. The midday water potential (ψ_midday) thus decreases far below the predawn level and may reach about 10 MPa.

In the continuum of water potentials between the soil and the atmosphere, water follows the water potential gradient (from high to lower potential, i.e. to increasingly more negative values), whereby the flow rate is limited by flow resistances depending on the characteristics of the soil and the types of tissue. In addition, there is a phase transition in the leaf from the liquid to the vapour phase at the site of evaporation in the leaf, with the rate of diffusion in the vapour phase being determined by the water vapour pressure of the atmosphere (e/e₀). In the soil-plant- atmosphere continuum (SPAC), the highest water potential gradient is between the cell walls of the leaf mesophyll where water evaporates and the atmospheric air, because of the extremely low water potential in the air (see Eq. 10.7 and Table 10.1). The physical description of leaf water status does not consider that the cellular water status might be additionally regulated by membrane-localised pores or valves—the aqua- porins (Chap. 6)—which facilitate water transport across lipophilic membranes.

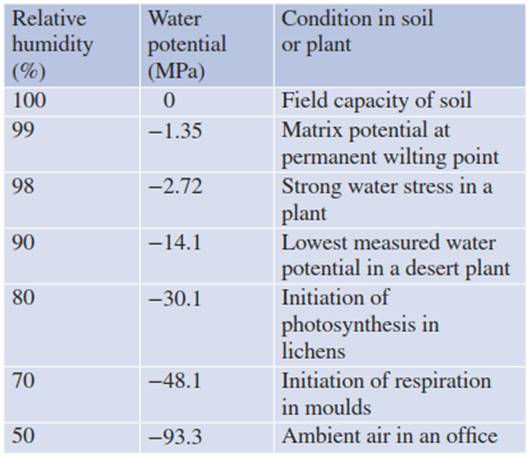
Table 10.1. Relationship between water potential and relative humidity. Following Eq. 10.7, air humidity can be measured in a closed vessel in which air equilibrates with salt solutions of different concentrations. Such an experiment can also be used to study particular processes—for example, moulds can establish at relative air humidity of >70%. (Walter and Kreeb 1970)

In a closed system, the water potential is related to the relative humidity of the surrounding air (see Eqs. 10.7 and 10.17). Thus, it is interesting to compare the relative air humidity with the water potential under equilibrium conditions, and various plant responses (Table 10.1). Most plants reach a permanent wilting point (Fig. 10.6) already at -1.5 MPa soil water potential when the relative humidity decreases to 99% inside the mesophyll. Photosynthesis is initiated in lichens at 80% relative humidity, and respiration in fruit moulds is activated at 70% relative humidity. Thus, the atmosphere is too dry for active live under average conditions.

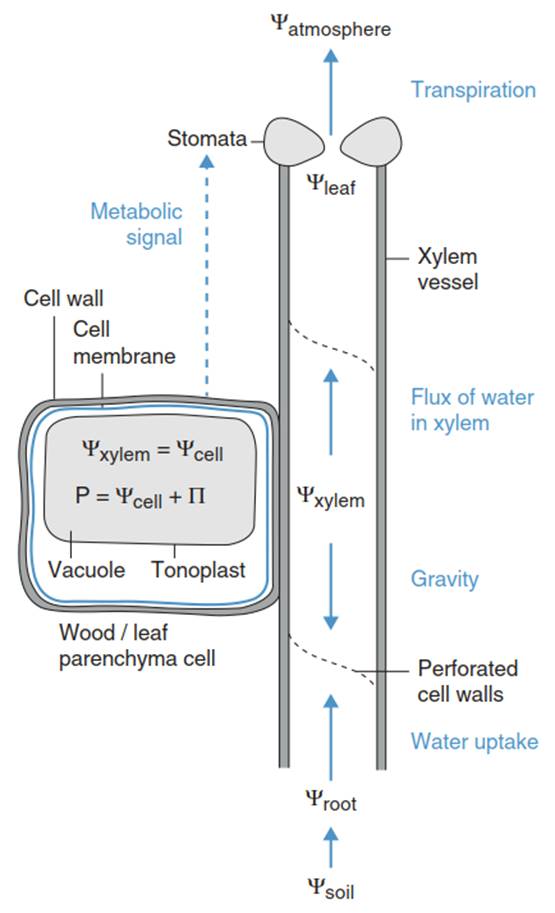
Fig. 10.5. Water status of a cell in a plant tissue

A cell in a plant tissue is embedded in a water potential gradient from the soil to the atmosphere as created by the water flow in the xylem, along a flow resistance (Fig. 10.5). The cell water potential equilibrates with the water potential in the xylem. Thus, the turgor pressure changes with the xylem water potential, and the cell may respond to these pressure changes by adjustment of the osmotic pressure in the vacuole. The water flow in the soil-plant-atmosphere continuum will be further discussed in Sect. 10.2.